题目内容
17.在平面直角坐标系xOy中,圆C的方程为x2+y2-6x+8=0,若直线y=2kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则实数k的取值范围是$[0,\frac{6}{5}]$.分析 由于圆C的方程为(x-3)2+y2=1,由题意可知,只需(x-3)2+y2=4与直线y=2kx-2有公共点即可.
解答 解:∵圆C的方程为x2+y2-6x+8=0,整理得:(x-3)2+y2=1,即圆C是以(3,0)为圆心,1为半径的圆;
又直线y=2kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C′:(x-3)2+y2=4与直线y=2kx-2有公共点即可.
设圆心C′(3,0)到直线y=2kx-2的距离为d,
则d=$\frac{|6k-2|}{\sqrt{4{k}^{2}+1}}$≤2,即5k2-6k≤0,
∴k∈$[0,\frac{6}{5}]$,
故答案为$[0,\frac{6}{5}]$.
点评 本题考查直线与圆的位置关系,将条件转化为“(x-3)2+y2=4与直线y=2kx-2有公共点”是关键,考查学生灵活解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{f(x-5)\\;x>2}\\{a{e}^{x}\\;x≤2}\end{array}\right.$,若f(2017)=e2,则a=( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
8.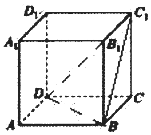 在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )
在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )
 在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )
在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
5.如图所示是用模拟方法估计圆周率π值的程序框图,m表示估计结果,则图中空白处应填入( )
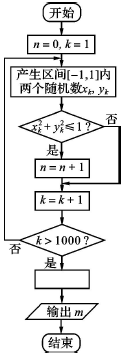

| A. | $m=\frac{n}{4000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=\frac{n}{500}$ | D. | $m=\frac{n}{250}$ |