题目内容
3.从年级抽取了21名考生在11月,02月两次月考的某科成绩进行统计,考生成绩均在[50,100]之间,发现这两次成绩高度正相关,考生成绩分布茎叶图如图: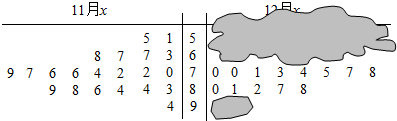
记每位考生的11月成绩为xi,12月成绩为yi,统计出:$\sum_{i=1}^{21}{x_i}=1575,\frac{1}{21}\sum_{i=1}^{21}{x_i^2}=5741,\sum_{i=1}^{21}{y_i}=1554,\frac{1}{21}\sum_{i=1}^{21}{{x_i}{y_i}}=5666$
由于统计老师的疏忽,统计表放在办公室被小猫抓坏,造成12月成绩中部分成绩茎叶图损坏(如图:
图中阴影区域),不知道统计人数和具体分数.凭记忆,知道12月成绩前三个分数段人数成等比数列,
后三个分数段人数成等差数列.
(1)求12月成绩在60分数段的人数,及12月成绩的样本中位数;
(2)计算两次月考成绩的回归方程,并预估11月考试成绩为88分的考生,在12月考试中的成绩.
注:$\widehat{b}$=$\frac{{\frac{1}{n}\sum_{i=1}^n{{x_1}{y_1}-\overline{xy}}}}{{\frac{1}{n}\sum_{i=1}^n{x_1^2-{{({\overline x})}^2}}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,742=5476,752=5625,762=577674•75=5550,75•76=5700.
分析 (1)利用12月成绩前三个分数段人数成等比数列,后三个分数段人数成等差数列,即可求12月成绩在60分数段的人数,及12月成绩的样本中位数;
(2)利用公式求出b,a,可得线性回归方程,即可得出结论.
解答 解:(1)∵后三个分数段人数成等差数列,
∴后三个分数段人数为8,5,2,
前两个分数段6人,
∵前三个分数段人数成等比数列,
∴前两个分数段人数分别为2,4,60分数段的人数为4,12月成绩的样本中位数为74;
(2)$\widehat{b}$=$\frac{5666-75•74}{5741-7{5}^{2}}$=1,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=74-75=-1,
∴y=x-1
∴x=88,y=87.
点评 本题考查线性回归方程,考查茎叶图,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
14.若p:a<1,q:关于x的二次方程x2+(a+1)x+a-2=0的一个根大于零,另一根小于零,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.语文、数学、英语共三本课本放成一摞,语文课本与数学课本恰好相邻放置的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |