题目内容
13.设定义在R上的奇函数y=f(x),满足对任意t∈R都有$f({\frac{1}{2}-t})=f({\frac{1}{2}+t})$,且x∈[0,$\frac{1}{2}$]时,f(x)=-x2,则f(3)+f(-$\frac{3}{2}$)的值等于( )| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{5}$ |
分析 对任意t∈R都有$f({\frac{1}{2}-t})=f({\frac{1}{2}+t})$,可得f(1-t)=f(t),又定义在R上的奇函数y=f(x),可得f(1+x)=f(-x)=-f(x),转化即可得出.
解答 解:∵对任意t∈R都有$f({\frac{1}{2}-t})=f({\frac{1}{2}+t})$,
∴f(1-t)=f(t),
又定义在R上的奇函数y=f(x),
∴f(1+x)=f(-x)=-f(x),
∴f(3)=-f(2)=f(1)=-f(0)=0,
$f(-\frac{3}{2})$=-$f(\frac{3}{2})$=$f(\frac{1}{2})$=$-(\frac{1}{2})^{2}$=-$\frac{1}{4}$.
∴f(3)+f(-$\frac{3}{2}$)=-$\frac{1}{4}$.
故选:C.
点评 本题考查了函数的奇偶性、对称性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
10.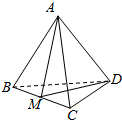 如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
 如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
11.方程x2+y2-2kx+(4k+10)y+20k+25=0(k∈R)表示的圆中,任意两个圆的位置关系是( )
| A. | 一定外切 | B. | 一定内切 | ||
| C. | 一定不相交 | D. | 不能确定,与k的值有关 |
1.设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|1<x<4},则∁u(A∪B)=( )
| A. | {0,1,2,3} | B. | {5} | C. | {1,2,4} | D. | {0,4,5} |
18.已知A(0,-2),B(3,2)是函数f(x)图象上的两点,且f(x)是R上的增函数,则|f(x)|<2的解集为( )
| A. | (1,4) | B. | (-1,2) | C. | (0,3) | D. | (3,4) |
5.设集合M={-2,0,2},N={x|x2=x},则M∩N=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {1} | D. | {0} |
6.将函数$f(x)=3sin(ωx-\frac{π}{5})(ω>0)$的图象向左平移$\frac{π}{5ω}$个单位,得到函数y=g(x)的图象,若y=g(x)在$[0,\frac{π}{4}]$上为增函数,则ω的最大值为( )
| A. | 2 | B. | $\frac{π}{5}$ | C. | 3 | D. | $\frac{2π}{5}$ |