题目内容
3.在△ABC中,$sinA=\frac{5}{13}$,$cosB=\frac{3}{5}$,若最大边长为63,则最小边长为25.分析 根据三角函数值推出角的范围,再分类讨论得到A是锐角,再根据两角和的正弦公式求出sinC,根据正弦定理即可求出a,问题得以解决.
解答 解:若A为钝角,
∵sinA=$\frac{5}{13}$<$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$>cosB=$\frac{3}{5}$>$\frac{1}{2}$,
∴150<A<180°,30°<B<60°,
∴A+B>180°,矛盾,
故A为锐角,
∵sinA=$\frac{5}{13}$<$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$>cosB=$\frac{3}{5}$>$\frac{1}{2}$,
∴0<A<30°<B<60°,且cosA=$\frac{12}{13}$,sinB=$\frac{4}{5}$
∴C为钝角,
∴c最大,最大为63,a最小,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{5}{13}$×$\frac{3}{5}$+$\frac{12}{13}$×$\frac{4}{5}$=$\frac{63}{65}$,
由正弦定理可得$\frac{a}{sinA}$=$\frac{c}{sinC}$,
∴a=$\frac{63}{\frac{63}{65}}$×$\frac{5}{13}$=25,故最小为a=25,
故答案为:25
点评 本题考查了同角的三角函数的关系和两角和的正弦公式和诱导公式,以及正弦定理,属于中档题

练习册系列答案
相关题目
18.如图是八位同学400米测试成绩的茎叶图(单位:秒),则( )


| A. | 平均数为64 | B. | 众数为7 | C. | 极差为17 | D. | 中位数为64.5 |
15.已知数列{an}满足a1=1,${a_2}=\frac{1}{3}$,若${a_n}({a_{n-1}}+2{a_{n+1}})=3{a_{n-1}}•{a_{n+1}}(n≥2,n∈{N^*})$,则数列{an}的通项an=( )
| A. | $\frac{1}{{{2^{n-1}}}}$ | B. | $\frac{1}{{{2^n}-1}}$ | C. | $\frac{1}{{{3^{n-1}}}}$ | D. | $\frac{1}{{{2^{n-1}}+1}}$ |
12.已知i是虚数单位,设1+ai=$\frac{2+bi}{i}$(a、b为实数),则a+bi在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.有三名男生和3名女生参加演讲比赛,每人依次按顺序出场比赛,若出场时相邻两个女生之间至少间隔一名男生,则共有( )种不同的排法.
| A. | 108 | B. | 120 | C. | 72 | D. | 144 |
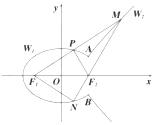 如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.
如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.