题目内容
4.函数$f(x)=\sqrt{x-1}+lg({x+1})$的定义域是( )| A. | (-1,1] | B. | (-1,1) | C. | [-1,1] | D. | [1,+∞) |
分析 根据函数的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:函数$f(x)=\sqrt{x-1}+lg({x+1})$,
∴$\left\{\begin{array}{l}{x-1≥0}\\{x+1>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x≥1}\\{x>-1}\end{array}\right.$,
即x≥1;
∴f(x)的定义域是[1,+∞).
故选:D.
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.设函数f(x)=2lnx-x2,则( )
| A. | x=e为极大值点 | B. | x=1为极大值点 | C. | x=1为极小值点 | D. | 无极值点 |
9.已知△ABC在正方形网格中的位置如图所示,则cos∠ABC=( )
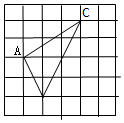

| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,已知△ABC,a、b分别为角A、B的对边,设A(bcosα,bsinα),∠AOB=β,D为线段AB的中点.
如图,已知△ABC,a、b分别为角A、B的对边,设A(bcosα,bsinα),∠AOB=β,D为线段AB的中点.