题目内容
(本题满分14分)设函数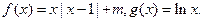 (1)当
(1)当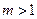 时,求函数
时,求函数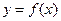 在
在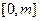 上的最大值;(2)记函数
上的最大值;(2)记函数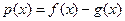 ,若函数
,若函数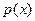 有零点,求
有零点,求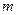 的取值范围.
的取值范围.
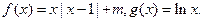 (1)当
(1)当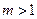 时,求函数
时,求函数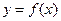 在
在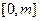 上的最大值;(2)记函数
上的最大值;(2)记函数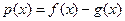 ,若函数
,若函数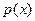 有零点,求
有零点,求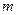 的取值范围.
的取值范围.(Ⅰ)当 时,
时,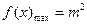 ,当
,当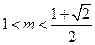 时,
时,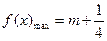 (Ⅱ)
(Ⅱ) 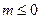
 时,
时,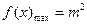 ,当
,当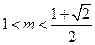 时,
时,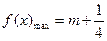 (Ⅱ)
(Ⅱ) 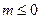
(1)当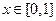 时,
时,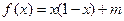 =
=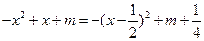
∴当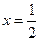 时,
时,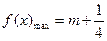 ------2分
------2分
当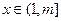 时,
时,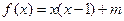 =
=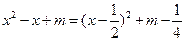
∵函数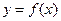 在
在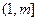 上单调递增 ∴
上单调递增 ∴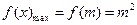 -----------4分
-----------4分
由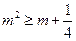 得
得 又
又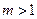
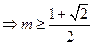
∴当 时,
时,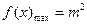 ,当
,当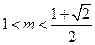 时,
时,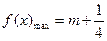 .----------6分
.----------6分
(2)函数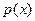 有零点即方程
有零点即方程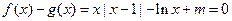 有解
有解
即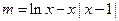 有解--7分令
有解--7分令 当
当 时
时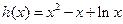
∵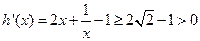 --------------9分
--------------9分
∴函数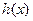 在
在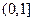 上是增函数,∴
上是增函数,∴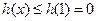 --------------10分
--------------10分
当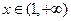 时,
时,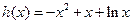
∵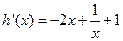
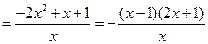
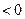 ------------12分
------------12分
∴函数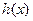 在
在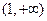 上是减函数,∴
上是减函数,∴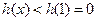 ----------------13分
----------------13分
∴方程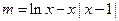 有解时
有解时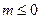 即函数
即函数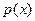 有零点时
有零点时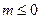 -------------14分
-------------14分
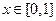 时,
时,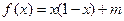 =
=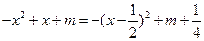
∴当
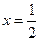 时,
时,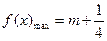 ------2分
------2分当
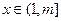 时,
时,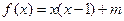 =
=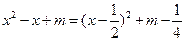
∵函数
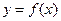 在
在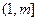 上单调递增 ∴
上单调递增 ∴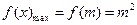 -----------4分
-----------4分由
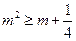 得
得 又
又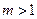
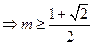
∴当
 时,
时,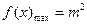 ,当
,当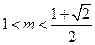 时,
时,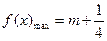 .----------6分
.----------6分(2)函数
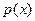 有零点即方程
有零点即方程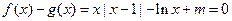 有解
有解即
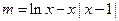 有解--7分令
有解--7分令 当
当 时
时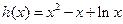
∵
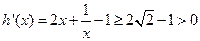 --------------9分
--------------9分∴函数
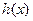 在
在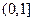 上是增函数,∴
上是增函数,∴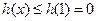 --------------10分
--------------10分当
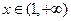 时,
时,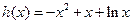
∵
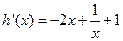
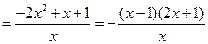
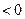 ------------12分
------------12分∴函数
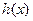 在
在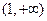 上是减函数,∴
上是减函数,∴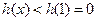 ----------------13分
----------------13分∴方程
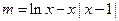 有解时
有解时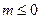 即函数
即函数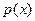 有零点时
有零点时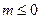 -------------14分
-------------14分
练习册系列答案
相关题目
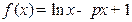

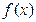 的极值点;
的极值点; ,求p的取值范围;
,求p的取值范围;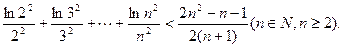
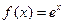 (
(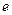 为自然对数的底数),
为自然对数的底数),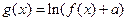 (
(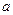 为常数),
为常数),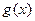 是实数集
是实数集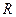 上的奇函数.(Ⅰ)求证:
上的奇函数.(Ⅰ)求证: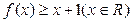 ;
;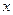 的方程:
的方程: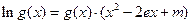
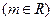 的根的个数;
的根的个数;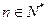 ,证明:
,证明: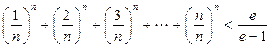 (
(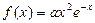 ,
,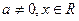 .
.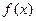 的单调性.
的单调性.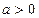 时,讨论关于
时,讨论关于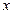 的方程
的方程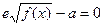 的实根的个数.
的实根的个数.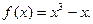
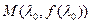 是函数图象上的一点,求点M处的切线方程;
是函数图象上的一点,求点M处的切线方程;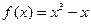 的三条切线。
的三条切线。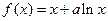 ,其中
,其中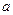 为常数,且
为常数,且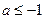 。
。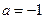 时,求
时,求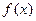 在
在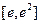 (
(
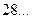 )上的值域;
)上的值域;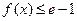 对任意
对任意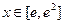 恒成立,求实数
恒成立,求实数 ,函数
,函数 ,
, .
. 的单调区间和值域;
的单调区间和值域; 若
若 ,总存在
,总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. 的极值情况下列描述正确的是( )
的极值情况下列描述正确的是( )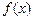 有极小值0
有极小值0
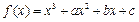 在
在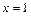 与
与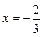 时都取得极值.
时都取得极值.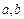 的值;(2)若
的值;(2)若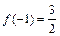 ,求
,求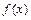 的单调区间和极值;
的单调区间和极值;