题目内容
7.a,b,c分别是△ABC角A,B,C的对边,△ABC的面积为$\sqrt{3}$,且$b=2,sinC=\frac{1}{2}$,则c=2或$2\sqrt{7}$.分析 由已知利用三角形面积公式可求a,利用同角三角函数基本关系式可求cosC的值,利用余弦定理即可解得c的值.
解答 解:∵$b=2,sinC=\frac{1}{2}$,S△ABC=$\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{1}{2}×a×2×\frac{1}{2}$,解得a=2$\sqrt{3}$,
∴cosC=$±\frac{\sqrt{3}}{2}$
∴利用余弦定理c2=a2+b2-2abcosC,可得:c=$12+4-2×2×2\sqrt{3}×(±\frac{\sqrt{3}}{2})$,
∴解得:c=2或$2\sqrt{7}$.
故答案为:2或$2\sqrt{7}$.(填写一个不给分)
点评 本题主要考查了三角形面积公式,同角三角函数基本关系式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,熟练掌握相关公式定理是解题的关键,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
17.已知{an}是公差为$\frac{1}{2}$的等差数列,Sn为{an}的前n项和,若a2,a6,a14成等比数列,则S5=( )
| A. | $\frac{35}{2}$ | B. | 35 | C. | $\frac{25}{2}$ | D. | 25 |
18.在递增的等差数列{an}中,a1+a5=1,a2a4=-12,则公差d为( )
| A. | $\frac{7}{2}$ | B. | -$\frac{7}{2}$ | C. | $\frac{7}{2}$或-$\frac{7}{2}$ | D. | 7或-7 |
2.在如图程序框图中,输入n=l,按程序运行后输出的结果为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.函数y=f(x)是实数集R上的偶函数,且在(-∞,0]上是单调递增函数,若f(a)≤f(2),则实数a的取值范围是( )
| A. | a≥-2 | B. | a≥2或a≤-2 | C. | -2≤a≤2 | D. | a≤2 |
16.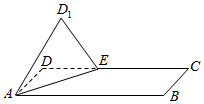 在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
 在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |