题目内容
12.函数y=f(x)是实数集R上的偶函数,且在(-∞,0]上是单调递增函数,若f(a)≤f(2),则实数a的取值范围是( )| A. | a≥-2 | B. | a≥2或a≤-2 | C. | -2≤a≤2 | D. | a≤2 |
分析 根据条件可知f(x)在[0,+∞)上单调递减,而根据f(x)为偶函数可得到f(|a|)≤f(2),从而便有|a|≥2,解该不等式即可得出实数a的取值范围.
解答 解:由题意得,f(x)在[0,+∞)上单调递减;
f(x)为R上的偶函数;
∴由f(a)≤f(2)得,f(|a|)≤f(2);
∴|a|≥2;
∴a≥2,或a≤-2.
故选:B.
点评 考查偶函数的定义,偶函数在对称区间上的单调性特点,以及绝对值不等式的解法,根据函数单调性解不等式的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列关于命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=3”是“函数f(x)=logax在定义域上为增函数”的充分不必要条件 | |
| C. | 若命题p:?n∈N,3n>100,则¬p:?n∈N,3n≤100 | |
| D. | 命题“?x∈(-∞,0),3x<5x”是真命题 |
4.平行直线l1:3x+4y-12=0与l2:6x+8y-15=0之间的距离为( )
| A. | $\frac{3}{10}$ | B. | $\frac{9}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{5}$ |
2.如图为某几何体的三视图,求该几何体的内切球的表面积为( )
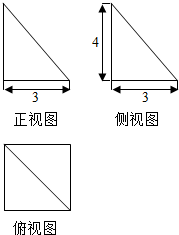

| A. | $\frac{1}{4}π$ | B. | 3π | C. | 4π | D. | $\frac{4}{3}π$ |
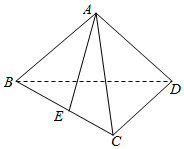 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.