题目内容
已知椭圆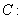
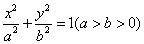 的左焦点为
的左焦点为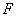 ,左、右顶点分别为
,左、右顶点分别为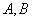 ,过点
,过点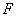 且倾斜角为
且倾斜角为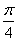 的直线
的直线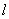 交椭圆于
交椭圆于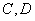 两点,椭圆
两点,椭圆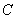 的离心率为
的离心率为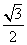 ,
,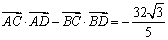 .
.
(1)求椭圆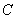 的方程;
的方程;
(2)若 是椭圆上不同两点,
是椭圆上不同两点,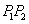
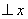 轴,圆
轴,圆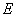 过点
过点 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆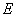 内,则称圆
内,则称圆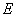 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆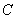 是否存在过点
是否存在过点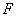 的内切圆?若存在,求出点
的内切圆?若存在,求出点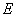 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1)因为离心率为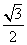 ,所以
,所以 ,
,
所以椭圆方程可化为: ,直线
,直线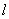 的方程为
的方程为 ,
,
由方程组 ,得:
,得: ,即
,即 ,
,
设 ,则
,则 ,
,
又 ,
,
所以 ,所以
,所以 ,椭圆方程是
,椭圆方程是 ;
;
(2)由椭圆的对称性,可以设 ,点
,点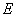 在
在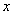 轴上,设点
轴上,设点 ,
,
则圆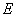 的方程为
的方程为 ,
,
由内切圆定义知道,椭圆上的点到点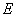 距离的最小值是
距离的最小值是 ,
,
设点 是椭圆
是椭圆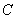 上任意一点,则
上任意一点,则 ,…9分
,…9分
当 时,
时, 最小,所以
最小,所以 ①
①
又圆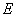 过点
过点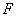 ,所以
,所以 ②
②
点 在椭圆上,所以
在椭圆上,所以 ③
③
由①②③解得: 或
或 ,
,
又 时,
时, ,不合,
,不合,
综上:椭圆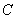 存在符合条件的内切圆,点
存在符合条件的内切圆,点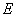 的坐标是
的坐标是 .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
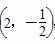 ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分. 上满足
上满足 的
的 的值有 个
的值有 个 的棱长为
的棱长为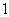 ,
,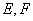 分别是棱
分别是棱 的中点,点
的中点,点 是
是 的动点,
的动点, ,过点
,过点 的平面将正方体分成上下两部分,记下面那部分的体积为
的平面将正方体分成上下两部分,记下面那部分的体积为 ,则函数
,则函数


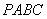 沿
沿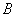 恰好经过原点.设顶点
恰好经过原点.设顶点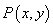 的轨迹方程是
的轨迹方程是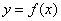 ,则对函数
,则对函数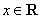 ,都有
,都有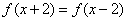 ;③函数
;③函数 上单调递减;④
上单调递减;④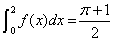 .其中判断正确的序号是 .
.其中判断正确的序号是 .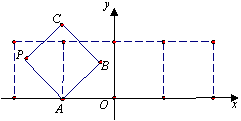
 中,
中, =
= ,则数列
,则数列 =( ).
=( ). 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( ) 的图像如图所示,则
的图像如图所示,则 的解集为 ( )
的解集为 ( ) B.
B. C.
C. D.
D.

 且被圆x2+y2=25截得的弦长是8,则该直线的方程为 ( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为 ( ).