题目内容
在直角坐标系xOy中,点M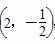 ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
(1)求m的值;
(2)过点M作直线l交抛物线C于A,B两点,设直线FA,FM,FB的斜率分别为k1,k2,k3,问k1,k2,k3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
解:(1)由题得抛物线C的焦点F的坐标为 ,线段MF的中点
,线段MF的中点
N 在抛物线C上,
在抛物线C上,
∴ -
-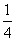 =m,8m2+2m-1=0,
=m,8m2+2m-1=0,
∴m=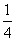 (m=-
(m=-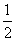 舍去).
舍去).
(2)由(1)知抛物线C:x2=4y,F(0,1).
设直线l的方程为y+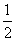 =k(x-2),
=k(x-2),
A(x1,y1),B(x2,y2),由
得x2-4kx+8k+2=0,
Δ=16k2-4(8k+2)>0,
∴
由根与系数的关系得
假设k1,k2,k3能成公差不为零的等差数列,则k1+k3=2k2.而k1+k3=

 =
= ,
,
k2= =-
=- ,
,
∴ =-
=- ,8k2+10k+3=0,
,8k2+10k+3=0,
解得k=-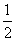 (符合题意)或k=-
(符合题意)或k=- (不合题意,舍去).
(不合题意,舍去).
∴直线l的方程为y+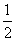 =-
=-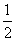 (x-2),
(x-2),
即x+2y-1=0.
∴k1,k2,k3能成公差不为零的等差数列,
此时直线l的方程为x+2y-1=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

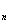 }为等差数列,且a
}为等差数列,且a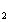 +a
+a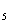 +a
+a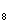 =
=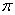 ,则
,则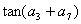 的值为( )
的值为( )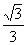 B.
B.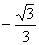 C.
C.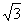 D.
D.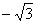
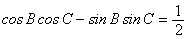 .
.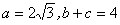 ,求△ABC的面积.
,求△ABC的面积.  -
- =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________. 为奇函数的
为奇函数的 的值可以是( )
的值可以是( ) B.
B. C.
C. D.
D.
 .
. B.-
B.- C.
C. D.
D.
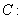
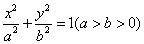 的左焦点为
的左焦点为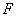 ,左、右顶点分别为
,左、右顶点分别为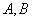 ,过点
,过点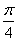 的直线
的直线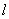 交椭圆于
交椭圆于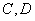 两点,椭圆
两点,椭圆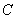 的离心率为
的离心率为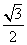 ,
,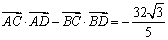 .
. 是椭圆上不同两点,
是椭圆上不同两点,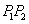
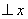 轴,圆
轴,圆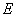 过点
过点