题目内容
16.以下四个命题中,真命题是( )| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
分析 A,当 (0,$\frac{π}{2}$)时,sinx<x<tanx,结合函数y=sinx与y=tanx的图象,不存在x∈(0,π),sinx=tanx;
对于B,“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1≤0,“;
C,当θ=k$π+\frac{π}{2}$,k∈Z时,函数f(x)=sin(2x+θ)是偶函数;
D,条件p 成立,条件q不一定成立,如x=1,y=6,条件pq成立,条件p一定成立.;
解答 解:对于A,因为当 (0,$\frac{π}{2}$)时,sinx<x<tanx,结合函数y=sinx与y=tanx的图象,不存在x∈(0,π),sinx=tanx,故错;
对于B,“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1≤0,故错”;
对于C,当θ=k$π+\frac{π}{2}$,k∈Z时,函数f(x)=sin(2x+θ)是偶函数,故错;
对于D,条件p 成立,条件q不一定成立,如x=1,y=6,条件pq成立,条件p一定成立.故正确;
故选:D
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
6.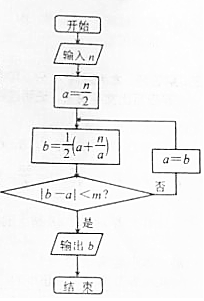 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
1.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{6}x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-ax,恰有三个不同的零点,则a的取值范围是( )
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |
8.已知向量$\overrightarrow{BA}=(1,-3)$,向量$\overrightarrow{BC}=(4,-2)$,则△ABC的形状为( )
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |
5.下列说法正确的是( )
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.