题目内容
17.函数f(x)=sinx-cosx,x∈[0,$\frac{π}{2}$]的最小值为-1.分析 先利用辅助角公式将函数化为y=Asin(ωx+φ)的形式,求出内层函数的取值范围,结合三角函数的图象和性质可得最小值.
解答 解:函数f(x)=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)
∵x∈[0,$\frac{π}{2}$],
∴x-$\frac{π}{4}$∈[$-\frac{π}{4}$,$\frac{π}{4}$]
∴当x-$\frac{π}{4}$=-$\frac{π}{4}$时,函数f(x)取得最小值-1.
故答案为:-1
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
8.某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据:
(1)求回归直线方程;
(2)据此估计广告费用为12万元时的销售额约为多少?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)据此估计广告费用为12万元时的销售额约为多少?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
9.已知sinθ=-$\frac{1}{3}$,且-π<θ<-$\frac{π}{2}$,则θ可表示为( )
| A. | $arcsin\frac{1}{3}$ | B. | $-\frac{π}{2}-arcsin(-\frac{1}{3})$ | C. | $-π+arcsin(-\frac{1}{3})$ | D. | $-π-arcsin(-\frac{1}{3})$ |
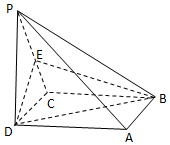 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,