题目内容
13.已知正四棱锥的底面边长为4cm,高与侧棱夹角为45°,则其斜高长为$2\sqrt{3}$(cm).分析 画出图来,根据斜高与高及底面底面边长的一半构成直角三角形求解.
解答  解:如图所示:∠SBO=45°,OE=2cm,SO=OB=2$\sqrt{2}$,
解:如图所示:∠SBO=45°,OE=2cm,SO=OB=2$\sqrt{2}$,
∴斜高为SE=$\sqrt{4+8}$-$2\sqrt{3}$,
故答案为$2\sqrt{3}$.
点评 本题主要考查棱锥的结构特征,主要涉及了棱锥基本量之间的关系.属基础题.

练习册系列答案
相关题目
5.抛物线y2=8x的焦点为F,设A(x1,y1),B(x2,y2)是抛物线上的两个动点,若x1+x2+4=$\frac{{2\sqrt{3}}}{3}|{AB}$|,
则∠AFB的最大值为( )
则∠AFB的最大值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
1.定义在R上的偶函数f(x)满足f(2-x)=f(x),且当x∈[1,2]时,f(x)=lnx-x+1,若函数g(x)=f(x)+mx有7个零点,则实数m的取值范围为( )
| A. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | B. | $(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | ||
| C. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})$ | D. | $(\frac{1-ln2}{8},\frac{ln2-1}{6})$ |
8.若命题¬(p∨q)为真命题,则下列说法正确的是( )
| A. | p为真命题,q为真命题 | B. | p为真命题,q为假命题 | ||
| C. | p为假命题,q为真命题 | D. | p为假命题,q为假命题 |
18.下列函数中,既是偶函数,又在区间(1,2)上是减函数的为( )
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D. | y=lg$\frac{2-x}{2+x}$ |
2.已知三个数a=0.60.3,b=log0.63,c=lnπ,则a,b,c的大小关系是( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
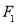 ,
,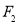 为椭圆
为椭圆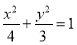 的左、右焦点,动点
的左、右焦点,动点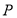 的坐标为
的坐标为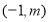 ,过点
,过点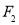 的直线与椭圆交于
的直线与椭圆交于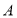 ,
, 两点.
两点.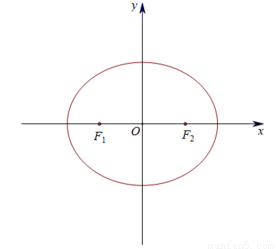
 ,
,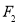 的坐标;
的坐标; ,
,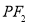 ,
,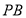 的斜率之和为0,求
的斜率之和为0,求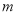 的所有整数值.
的所有整数值.