题目内容
已知O是坐标原点，点A（-1，0），若M（x，y）为平面区域
上的一个动点，则|
+
|的取值范围是（ ）
|
| OA |
| OM |
A、[1，
| ||
B、[2，
| ||
| C、[1，2] | ||
D、[0，
|
考点：简单线性规划
专题：不等式的解法及应用
分析：由题意作出可行域，由向量的坐标加法运算求得+的坐标，把||转化为可行域内的点M（x，y）到定点N（1，0）的距离，数形结合可得答案．
解答：
解：
+
=（-1，0）+（x，y）=（x-1，y），
则|
+
|=
，
设z=|
+
|=
，
则z的几何意义为M到定点D（1，0）的距离，
由约束条件作平面区域如图，
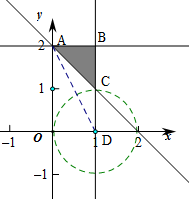
由图象可知当M位于A（0，2）时，z取得最大值z=
=
，
当M位于C（1，1）时，z取得最小值z=1，
1≤z≤
，
即|
+
|的取值范围是[1，
]，
故选：A
| OA |
| OM |
则|
| OA |
| OM |
| (x-1)2+y2 |
设z=|
| OA |
| OM |
| (x-1)2+y2 |
则z的几何意义为M到定点D（1，0）的距离，
由约束条件作平面区域如图，
由图象可知当M位于A（0，2）时，z取得最大值z=
| 1+4 |
| 5 |
当M位于C（1，1）时，z取得最小值z=1，
1≤z≤
| 5 |
即|
| OA |
| OM |
| 5 |
故选：A
点评：本题考查了简单的线性规划，考查了数形结合、转化与化归等解题思想方法，考查了向量模的求法，是中档题．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
下列各组函数中，表示同一函数的是（ ）
A、f（x）=
| ||
B、f（x）=|x|与g（x）=
| ||
C、f（x）=x与g（x）=（
| ||
D、y=
|
若等差数列{an}满足：
＜-1，且公差d＜0，其前n项和为Sn．则满足Sn＞0的n的最大值为（ ）
| a11 |
| a12 |
| A、11 | B、22 | C、19 | D、20 |
复数z满足方程|z+（1-i）|=2，那么复数z的对应点P组成的图形为（ ）
| A、以（1，-1）为圆心，4为半径的圆 |
| B、以（1，-1）为圆心，2为半径的圆 |
| C、以（-1，1）为圆心，4为半径的圆 |
| D、以（-1，1）为圆心，2为半径的圆 |
椭圆的中心在坐标原点，F为左焦点，B为上顶点，A为右顶点，当FB⊥AB时，此类椭圆被称为“黄金椭圆”，其离心率为
，类比“黄金椭圆”可推算出“黄金双曲线”的离心率为（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若lga，lgb，lgc三数成等差数列，则（ ）
A、b=
| ||
B、b=±
| ||
| C、a，b，c成等比数列 | ||
| D、a，b，c成等差数列 |
已知函数f（x）=（a-x）（x-b）-3，m，n是方程f（x）=0的两个实根，其中a＜b，m＜n，则实数a，b，m，n的大小关系是（ ）
| A、a＜m＜b＜n |
| B、m＜a＜n＜b |
| C、m＜a＜b＜n |
| D、a＜m＜n＜b |
如图是一结构图，在
处应填入（ ）
处应填入（ ）| A、合情推理 | B、三段论推理 |
| C、类比推理 | D、归纳推理 |