题目内容
已知等腰三角形的顶角的余弦值等于-
，求这个三角形的底角的正弦、余弦和正切的值．
| 7 |
| 25 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：如图所示，△ABC为等腰三角形，AB=AC，且AD⊥BC，可得AD平分∠BAC，由题意得到顶角的余弦值，利用二倍角的余弦函数公式化简，整理求出cos∠BAD的值，即可确定出sinB，cosB，以及tanB的值．
解答：
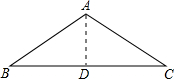解：如图所示，△ABC为等腰三角形，AB=AC，且AD⊥BC，可得AD平分∠BAC，即∠BAD=∠CAD=
∠BAC，
根据题意得：cos∠BAC=-
，即2cos2∠BAD-1=-
，
整理得：cos2∠BAD=
，即cos∠BAD=
，
在Rt△ABD中，cos∠BAD=
，
∴sinB=
，cosB=
=
，tanB=
=
．
解：如图所示，△ABC为等腰三角形，AB=AC，且AD⊥BC，可得AD平分∠BAC，即∠BAD=∠CAD=| 1 |
| 2 |
根据题意得：cos∠BAC=-
| 7 |
| 25 |
| 7 |
| 25 |
整理得：cos2∠BAD=
| 9 |
| 25 |
| 3 |
| 5 |
在Rt△ABD中，cos∠BAD=
| 3 |
| 5 |
∴sinB=
| 3 |
| 5 |
| 1-sin2B |
| 4 |
| 5 |
| sinB |
| cosB |
| 3 |
| 4 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
已知3x=10，则这样的x（ ）
| A、存在且只有一个 |
| B、存在且不只一个 |
| C、存在且x＜2 |
| D、根本不存在 |
“m≥8”是“方程x2-mx+2m=0有两个大于2的根”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f（x）=loga（2-ax）在（-∞，1]上单调递减，则a的取值范围是（ ）
| A、（1，2） |
| B、（0，1） |
| C、（0，1）∪（1，2） |
| D、（0，1）∪（2，+∞） |