题目内容
7.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(0,1),则当$t∈[-\sqrt{3},2]$时,|$\overrightarrow{a}$-t•$\overrightarrow{b}$|的取值范围是[1,$\sqrt{13}$].分析 计算|$\overrightarrow{a}-t\overrightarrow{b}$|2,根据t的范围求出|$\overrightarrow{a}-t\overrightarrow{b}$|2的最值,开方得出|$\overrightarrow{a}-t\overrightarrow{b}$|的最值.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$,${\overrightarrow{a}}^{2}=4$,${\overrightarrow{b}}^{2}=1$.
∴|$\overrightarrow{a}-t\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}+{t}^{2}{\overrightarrow{b}}^{2}-2t\overrightarrow{a}•\overrightarrow{b}$=t2-2$\sqrt{3}$t+4=(t-$\sqrt{3}$)2+1.
∴当t=$\sqrt{3}$时,|$\overrightarrow{a}-t\overrightarrow{b}$|2取得最小值1,当t=-$\sqrt{3}$时,|$\overrightarrow{a}-t\overrightarrow{b}$|2取得最大值13.
∴|$\overrightarrow{a}-t\overrightarrow{b}$|的最小值为1,|$\overrightarrow{a}-t\overrightarrow{b}$|的最大值为$\sqrt{13}$.
故答案为:$[1,\sqrt{13}]$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
10.已知集合A={x|x2-4x<0},B={x|-1≤x≤1},则A∪B=( )
| A. | [-1,1] | B. | [-1,4) | C. | (0,1] | D. | (0,4) |
2.已知等差数列{an}的前n项和为Sn,公差为d,若$\frac{{S}_{2016}}{2016}$-$\frac{{S}_{16}}{16}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
17.设点(x,y)在平面区域E内,记事件A“对任意(x,y)∈E,有2x-y≥1”,则满足事件A发生的概率P(A)=1的平面区域E可以是( )
| A. | $\left\{\begin{array}{l}{x≤2}\\{x+y≥0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x+y≤0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥2}\\{x-y≤0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤2}\\{x-y≥0}\end{array}\right.$ |
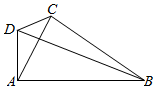 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.