题目内容
16.若sinθ+coθ=$\frac{2}{3}$,则sinθ-cosθ=( )| A. | $\frac{\sqrt{14}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | ±$\frac{\sqrt{14}}{3}$ | D. | ±$\frac{\sqrt{6}}{3}$ |
分析 利用同角三角的基本关系,求得2sinθcosθ的值,再根据sinθ-cosθ=±$\sqrt{{(sinθ-cosθ)}^{2}}$=±$\sqrt{1-2sinθcosθ}$,求得sinθ-cosθ的值.
解答 解:∵sinθ+coθ=$\frac{2}{3}$,∴1+2sinθcosθ=$\frac{4}{9}$,∴2sinθcosθ=-$\frac{5}{9}$,∴sinθ和cosθ异号,
则sinθ-cosθ=±$\sqrt{{(sinθ-cosθ)}^{2}}$=±$\sqrt{1-2sinθcosθ}$=±$\sqrt{\frac{14}{9}}$=±$\frac{\sqrt{14}}{3}$,
故选:C.
点评 本题主要考查同角三角的基本关系,属于基础题.

练习册系列答案
相关题目
4.若集合A={x|y=(x-1)0},B={y|y=x2,x∈R},则A∩B等于( )
| A. | {x|-1≤x≤1} | B. | {x|x≥0} | C. | {x|x≥0且x≠1} | D. | ∅ |
1.运行如图所示的程序框图,若输出的点恰有3次落在直线上y=x,则判断框中可填写的条件是( )
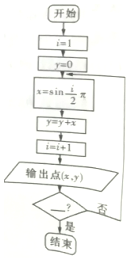

| A. | i>8 | B. | i>7 | C. | i>6 | D. | i>5 |