题目内容
若球的半径为R,作内接于球的圆柱,则其侧面积的最大值为( )
| A、2πR2 | ||
| B、πR2 | ||
| C、4πR2 | ||
D、
|
考点:旋转体(圆柱、圆锥、圆台)
专题:不等式的解法及应用,空间位置关系与距离
分析:由题意圆柱的底面为球的截面,由球的截面性质可得出圆柱的高为h、底面半径为r与球的半径为R的关系,再用h和r表示出圆柱的侧面积,利用基本不等式求最值即可.
解答:
解:如图为轴截面,令圆柱的高为h,

底面半径为r,侧面积为S,
则(
)2+r2=R2,
即h=2
.
∵圆柱的侧面积S=2πrh=4πr•
=4π
≤4π
=2πR2,
故选:A

底面半径为r,侧面积为S,
则(
| h |
| 2 |
即h=2
| R2-r2 |
∵圆柱的侧面积S=2πrh=4πr•
| R2-r2 |
| r2(R 2-r2) |
|
故选:A
点评:本题考查球与圆柱的组合体问题、以及利用基本不等式求最值问题,难度一般.

练习册系列答案
相关题目
对于事件A和事件B,通过计算得到K2的观测值k≈4.526,下列说法正确的是( )
| A、在犯错误的概率不超过0.01的前提下认为事件A和事件B有关 |
| B、在犯错误的概率不超过0.05的前提下认为事件A和事件B有关 |
| C、在犯错误的概率不超过0.01的前提下认为事件A和事件B无关 |
| D、在犯错误的概率不超过0.05的前提下认为事件A和事件B无关 |
已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A、f(1)<ef(0),f(2014)<e2014f(0) |
| B、f(1)>ef(0),f(2014)>e2014f(0) |
| C、f(1)>ef(0),f(2014)<e2014f(0) |
| D、f(1)<ef(0),f(2014)>e2014f(0) |
甲、乙两人一起去游海口车展,他们约定各自独立的从1到6号展台中,任选4个进行观看,每个展台参观10分钟,则最后10分钟他们同在一个展台的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=cosx(0≤x≤π)与y=-1围成的面积是( )
| A、0 | B、2 | C、4 | D、6 |
已知x,y为实数,若3x+5y>3-y+5-x,则( )
| A、x+y>0 |
| B、x+y<0 |
| C、x-y<0 |
| D、x-y>0 |
若a?α,b?α,a∥α,条件甲是“a∥b”,条件乙是“b∥α”,则条件甲是条件乙的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
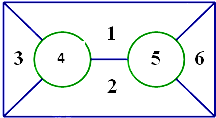 有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )| A、4320 | B、2880 |
| C、1440 | D、720 |