题目内容
16.$\frac{tan40°}{1-ta{n}^{2}40°}$=$\frac{1}{2}$tan80°.分析 根据二倍角的正切函数公式,进行化简即可.
解答 解:$\frac{tan40°}{1{-tan}^{2}40°}$=$\frac{1}{2}$•$\frac{2tan40°}{1{-tan}^{2}40°}$
=$\frac{1}{2}$tan80°.
故答案为:$\frac{1}{2}$tan80°.
点评 本题考查了二倍角的正切公式的逆用问题,是基础题目.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若$\frac{h(x)-g(x)}{x-{x}_{0}}$>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=lnx+x2-x的“类对称点”的横坐标是( )
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
1.已知集合A={1,-1},B={-1,0},C={1,2},则(A∩B)∪C=( )
| A. | {-1,0,1} | B. | {-1,1} | C. | {-1,1,2} | D. | {1,0} |
12.复数z=-3+(1+i)2在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
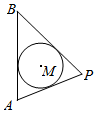 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.