题目内容

8．已知函数f（x）=1g$\frac{2+x}{2-x}$，求此函数的定义域并判断此函数的奇偶性．

分析 （1）根据对数的函数的概念，只要真数大于零即可；（2）根据函数奇偶性的概念判断即可．

解答 解：（1）因为函数f（x）=lg$\frac{2+x}{2-x}$，
所以应满足$\frac{2+x}{2-x}$＞0，解得：-2＜x＜2，
所以函数f（x）的定义域是（-2，2）；
（2）由于函数f（x）的定义域是（-2，2）；
所以f（-x）=lg $\frac{2-x}{2+x}$=-lg $\frac{2+x}{2-x}$=-f（x），
故函数f（x）是奇函数．

点评 本题主要考查函数的定义域和函数的单调性，属于基础题．

练习册系列答案
相关题目
18．已知数列{an}满足a2=2，且数列{3an-2n}为公比为2的等比数列，则a1=1，数列{an}通项公式an=$\frac{2n+{2}^{n-1}}{3}$．
19．在△ABC中，a=5，b=4，sin$\frac{C}{2}$=$\frac{4}{5}$，求△ABC的面积S．
16．$\frac{tan40°}{1-ta{n}^{2}40°}$=$\frac{1}{2}$tan80°．
3．某种商品进价为600元，标价900元，现在商店准备打折销售，但要保证利润不低于120元，则至少可以打（　　）折？
A．6折B．7折C．8折D．9折
13．不等式-1≤tan（$\frac{x}{2}$-$\frac{π}{3}$）≤$\sqrt{3}$的解集为[$\frac{π}{6}$+2kπ，2kπ+$\frac{4π}{3}$]，k∈Z．
6．设a，b是两条不同的直线，α，β是两个不同的平面，则下列四个命题中，正确命题的个数是（　　）
①若a⊥b，a⊥α，则b∥α； 
②若a∥α，α⊥β，则a∥β；
③若a⊥β，α⊥β，则a∥α；
④若a∥b，a∥α，b∥β，则α∥β．
A．3B．2C．1D．0
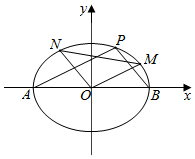3．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点P（1，$\frac{\sqrt{6}}{2}$），且离心率等于$\frac{\sqrt{2}}{2}$．点A，B分别为椭圆C的左、右顶点，M，N是椭圆C上非顶点的两点，且△OMN的面积等于$\sqrt{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点A作AP∥OM交椭圆C于点P，求证：BP∥ON．
4．己知两点A（2，0），B（-2，0），直线l过点B且与x轴垂直，点C是l上异于点B的动点，直线BP垂直线段OC并交线段AC于点P，记点P的轨迹为曲线Γ．
（1）求曲线Γ的方程；
（2）过点D（-1，0）的直线与曲线 Γ交于M，N两点，直线AM，AN分别与l交于E，F两点．当△AEF的面积是△AMN的面积的2倍时，求直线MN的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网