题目内容
7.设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若$\frac{h(x)-g(x)}{x-{x}_{0}}$>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=lnx+x2-x的“类对称点”的横坐标是( )| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 函数y=f(x)在其图象上一点P(x0,f(x0))处的切线方程为y=g(x))=(2x0+$\frac{1}{{x}_{0}}$-1)(x-x0)+x02-x0+lnx0,由此能推导出y=f(x)存在“类对称点”,$\frac{\sqrt{2}}{2}$是一个“类对称点”的横坐标.
解答 解:函数y=f(x)在其图象上一点P(x0,f(x0))处的切线方程为:
y=g(x)=(2x0+$\frac{1}{{x}_{0}}$-1)(x-x0)+x02-x0+lnx0,
设m(x)=f(x)-g(x)=x2-x+lnx-(2x0+$\frac{1}{{x}_{0}}$-1)(x-x0)-x02+x0-lnx0,
则m(x0)=0.
m′(x)=2x+$\frac{1}{x}$-1-(2x0+$\frac{1}{{x}_{0}}$-1)=(x-x0)(2-$\frac{1}{x{x}_{0}}$)=$\frac{1}{x}$(x-x0)(2x-$\frac{1}{{x}_{0}}$)
若x0<$\frac{\sqrt{2}}{2}$,m(x)在(x0,$\frac{1}{2{x}_{0}}$)上单调递减,
∴当x∈(x0,$\frac{1}{2{x}_{0}}$)时,m(x)<m(x0)=0,此时$\frac{m(x)}{x-{x}_{0}}$<0;
若x0>$\frac{\sqrt{2}}{2}$,φ(x)在($\frac{1}{2{x}_{0}}$,x0)上单调递减,
∴当x∈($\frac{1}{2{x}_{0}}$,x0)时,m(x)>m(x0)=0,此时时$\frac{m(x)}{x-{x}_{0}}$<0;
∴y=f(x)在(0,$\frac{\sqrt{2}}{2}$)∪($\frac{\sqrt{2}}{2}$,+∞)上不存在“类对称点”.
若x0=$\frac{\sqrt{2}}{2}$,$\frac{2}{x}$(x-$\frac{\sqrt{2}}{2}$)2>0,
∴m(x)在(0,+∞)上是增函数,
当x>x0时,m(x)>m(x0)=0,
当x<x0时,m(x)<m(x0)=0,故$\frac{m(x)}{x-{x}_{0}}$>0.
即此时点P是y=f(x)的“类对称点”
综上,y=f(x)存在“类对称点”,$\frac{\sqrt{2}}{2}$是一个“类对称点”的横坐标.
故选:B.
点评 本题考查函数的单调增区间的求法,探索满足函数在一定零点下的参数的求法,探索函数是否存在“类对称点”.解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用,此题是难题.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
| A. | [$\frac{1}{e}$,e] | B. | ($\frac{2}{e}$,e] | C. | ($\frac{2}{e}$,+∞) | D. | ($\frac{2}{e}$,e+$\frac{1}{e}$) |
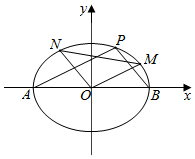 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(1,$\frac{\sqrt{6}}{2}$),且离心率等于$\frac{\sqrt{2}}{2}$.点A,B分别为椭圆C的左、右顶点,M,N是椭圆C上非顶点的两点,且△OMN的面积等于$\sqrt{2}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(1,$\frac{\sqrt{6}}{2}$),且离心率等于$\frac{\sqrt{2}}{2}$.点A,B分别为椭圆C的左、右顶点,M,N是椭圆C上非顶点的两点,且△OMN的面积等于$\sqrt{2}$.