题目内容
16．设全集U={x|x是小于10的正整数}，B={1，2，3，4}，C={3，4，5，6}，求（1）用列举法表示全集U
（2）D=B∩C，则写出集合D的所有子集
（3）∁U（B∩C）
分析 （1）用列举法写出全集U即可，
（2）写出D=B∩C，再写出集合D的所有子集；
（3）根据补集的定义写出∁U（B∩C）．
解答 解：（1）全集U={x|x是小于10的正整数}
={1，2，3，4，5，6，7，8，9}，
（2）B={1，2，3，4}，C={3，4，5，6}，
D=B∩C={3，4}，
∴集合D的所有子集是∅，{3}，{4}，{3，4}；
（3）∁U（B∩C）={1，2，5，6，7，8，9}．
点评 本题考查了集合的定义与应用问题，是基础题目．
练习册系列答案
相关题目
7．若变量x，y满足$\left\{{\begin{array}{l}{x+y≤2}\\{2x-3y≤9}\\{x≥0}\end{array}}\right.$则z=（x+1）2+y2的最大值是（ ）
| A． | 12 | B． | 10 | C． | 17 | D． | 26 |
4．《九章算术》中的“两鼠穿墙题”是我国数学的古典名题：“今有垣厚若干尺，两鼠对穿，大鼠日一尺，小鼠也日一尺．大鼠日自倍，小鼠日自半．问何日相逢，各穿几何？题意是：有两只老鼠从墙的两边打洞穿墙．大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半”如果墙足够厚，Sn为前n天两只老鼠打洞长度之和，则S5=（ ）
| A． | $31\frac{15}{16}$ | B． | $32\frac{15}{16}$ | C． | $33\frac{15}{16}$ | D． | $26\frac{1}{2}$ |
11．若集合A={x|x2≤0}，则下列结论中正确的是（ ）
| A． | A=0 | B． | 0⊆A | C． | A=∅ | D． | {0}⊆A |
6．
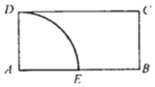如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）
如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）| A． | $\frac{π}{8}$ | B． | 1-$\frac{π}{8}$ | C． | $\frac{π}{4}$ | D． | 1-$\frac{π}{4}$ |