题目内容
某种放射性元素,100年后只剩原来的一半.现有这种元素1克,3年后剩下 克.
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由半衰期为100年,得到3年所占半衰期,则由n=1×(
)
求得1克元素3年后的剩余量.
| 1 |
| 2 |
| 3 |
| 100 |
解答:
解:此元素半衰期为100年,3年占了
个半衰期,
则1克元素3年后剩下n=1×(
)
=0.979克.
故答案为:0.979.
| 3 |
| 100 |
则1克元素3年后剩下n=1×(
| 1 |
| 2 |
| 3 |
| 100 |
故答案为:0.979.
点评:本题考查了等比数列的通项公式,关键是对题意的理解,是基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设数列{an}是等差数列,公差d>0,Sn为其前n项和,若正整数i,j,k,l满足i<k<l<j,且i+j=k+l,则( )
| A、Si+Sj<Sk+Sl |
| B、Si+Sj>Sk+Sl |
| C、SiSj<SkSl |
| D、SiSj>SkSl |
设复数z=-1-i(i为虚数单位),则|1-z|=( )
A、
| ||
B、
| ||
| C、2 | ||
| D、1 |
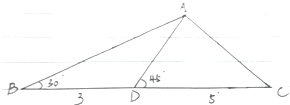 在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.
在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.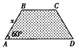 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9