题目内容
1.已知cosα-sinα=$\frac{3\sqrt{2}}{5}$(π<α<$\frac{3π}{2}$),则$\frac{sin2α(1+tanα)}{1-tanα}$=( )| A. | -$\frac{28}{75}$ | B. | $\frac{28}{75}$ | C. | -$\frac{56}{75}$ | D. | $\frac{56}{75}$ |
分析 把已知的等式两边平方求得2sinαcosα=$\frac{7}{25}$,结合α的范围求得sinα+cosα,化简$\frac{sin2α(1+tanα)}{1-tanα}$后代入得答案.
解答 解:∵cosα-sinα=$\frac{3\sqrt{2}}{5}$,平方可得1-2sinαcosα=$\frac{18}{25}$,
∴2sinαcosα=$\frac{7}{25}$.
又α∈(π,$\frac{3π}{2}$),故sinα+cosα=-$\sqrt{(sinα+cosα)^{2}}$=-$\sqrt{1+2sinαcosα}$=-$\frac{4\sqrt{2}}{5}$,
∴$\frac{sin2α(1+tanα)}{1-tanα}$=$\frac{2sinαcosα(cosα+sinα)}{cosα-sinα}$=$\frac{\frac{7}{25}×(-\frac{4\sqrt{2}}{5})}{\frac{3\sqrt{2}}{5}}$=$-\frac{28}{75}$.
故选:A.
点评 本题考查了同角三角函数基本关系的应用,考查了学生的计算能力,是中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
12.已知a=$\sqrt{0.4}$,b=20.4,c=0.40.2,则a,b,c三者的大小关系是( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>b>a |
13.下列命题中为真命题的是( )
| A. | 命题“若x>1,则x2>1”的否命题 | B. | 命题“若x>y,则x>|y|”的逆命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2≥1,则x≥1”的逆否命题 |
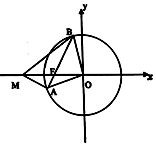 已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.
已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB. 某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.
某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.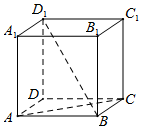 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.