题目内容
11.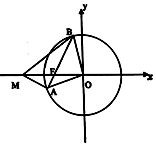 已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.
已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.(1)求△AOB面积的最大值及取得最大值时直线AB的方程;
(2)若点M在x轴上,且使得MF为△AMB的一条内角平方线,求点M的坐标.
分析 (1)设∠AOB=θ,则${S_{△AOB}}=\frac{1}{2}|OA|•|OB|sinθ=\frac{1}{2}×4×4×sinθ=8sinθ$,即可求△AOB面积的最大值及取得最大值时直线AB的方程;
(2)分类讨论,由$\left\{\begin{array}{l}y=k(x+3)\\{x^2}+{y^2}=16\end{array}\right.$得:(1+k2)x2+6k2x+(9k2-16)=0,利用∠BMF=∠AMF,kBM+kAM=0,即可得出结论.
解答 解:(1)设∠AOB=θ,则${S_{△AOB}}=\frac{1}{2}|OA|•|OB|sinθ=\frac{1}{2}×4×4×sinθ=8sinθ$,
当$θ=\frac{π}{2}$时,S△AOBmax=8,此时O到AB的距离为$2\sqrt{2}<3$,${k_{AB}}=±2\sqrt{2}$,
∴S△AOBmax=8,直线AB的方程为$y=±2\sqrt{2}(x+3)$.
(2)当直线AB斜率不存在时,MF始终平分∠AMB.
当直线AB斜率存在时,设直线AB:y=k(x+3),(k≠0),设M(m,0),
由$\left\{\begin{array}{l}y=k(x+3)\\{x^2}+{y^2}=16\end{array}\right.$得:(1+k2)x2+6k2x+(9k2-16)=0
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=\frac{{-6{k^2}}}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{9{k^2}-16}}{{1+{k^2}}}$.
∵∠BMF=∠AMF,
∴kBM+kAM=0,${k_{BM}}+{k_{AM}}=\frac{y_1}{{{x_1}-m}}+\frac{y_2}{{{x_2}-m}}=\frac{{k({x_1}+3)}}{{{x_1}-m}}+\frac{{k({x_2}+3)}}{{{x_2}-m}}=0$,
∴(x1+3)(x2-m)+(x2+3)(x1-m)=0,
∴2x1x2+(3-m)(x1+x2)-6m=0,
∴$2×\frac{{9{k^2}-16}}{{1+{k^2}}}+(3-m)×\frac{{-6{k^2}}}{{1+{k^2}}}-6m=0$,
∴-32-6m=0,$m=-\frac{16}{3}$,
∴$M(-\frac{16}{3},0)$.
点评 本题考查三角形面积的计算,考查直线与圆的位置关系,考查韦达定理的运用,考查分类讨论的数学思想,属于中档题.

| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
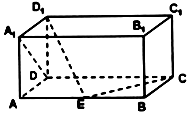 如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°. | A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
| A. | -$\frac{28}{75}$ | B. | $\frac{28}{75}$ | C. | -$\frac{56}{75}$ | D. | $\frac{56}{75}$ |
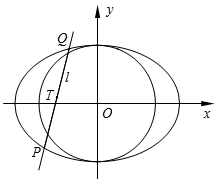 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.