题目内容
16.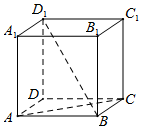 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.( I)求证:AC⊥BD1;
(Ⅱ)是否存在直线与直线 AA1,CC1,BD1都相交?若存在,请你在图中画出两条满足条件的直线(不必说明画法及理由);若不存在,请说明理由.
分析 (Ⅰ)连结BD,推导出D1D⊥AC,AC⊥BD.由此能证明AC⊥BD1.
(Ⅱ)作出满足条件的直线一定在平面ACC1A1中,且过BD1的中点并与直线A1A,C1C相交.
解答 (本题满分9分)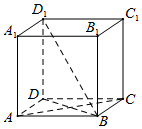
(Ⅰ)证明:如图,连结BD.
∵正方体ABCD-A1B1C1D1,
∴D1D⊥平面ABCD.
∵AC?平面ABCD,∴D1D⊥AC.
∵四边形ABCD是正方形,∴AC⊥BD.
∵BD∩D1D=D,∴AC⊥平面BDD1.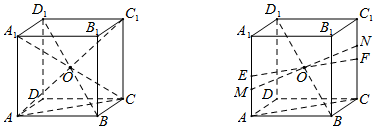
∵BD1?平面BDD1,∴AC⊥BD1.…(5分)
(Ⅱ)存在.答案不唯一,
作出满足条件的直线一定在平面ACC1A1中,
且过BD1的中点并与直线A1A,C1C相交.
下面给出答案中的两种情况,
其他答案只要合理就可以给满分.(9分)
点评 本题考查线线垂直的证明,考查满足条件的直线的作法,是中档题,解题时要认真题、注意空间思维能力的培养.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.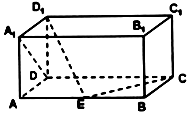 如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
 如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
11.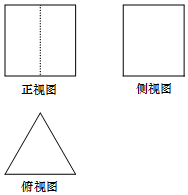 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
1.已知cosα-sinα=$\frac{3\sqrt{2}}{5}$(π<α<$\frac{3π}{2}$),则$\frac{sin2α(1+tanα)}{1-tanα}$=( )
| A. | -$\frac{28}{75}$ | B. | $\frac{28}{75}$ | C. | -$\frac{56}{75}$ | D. | $\frac{56}{75}$ |
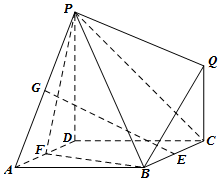 如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.
如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.