题目内容
5.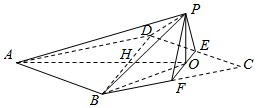 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.(Ⅰ) 求证:BD⊥PA;
(Ⅱ) 求二面角B-AP-O的正切值.
分析 (Ⅰ)根据面面垂直的性质定理即可证明BD⊥PA;
(Ⅱ) 建立空间坐标系,求出平面的法向量,利用向量法即可求二面角B-AP-O的正切值.
解答  证明:(1)因为平面PEF⊥平面ABD,平面PEF∩平面ABD=EF,PO?PEF,
证明:(1)因为平面PEF⊥平面ABD,平面PEF∩平面ABD=EF,PO?PEF,
∴PO⊥ABD
则PO⊥BD,又AO⊥BD,AO∩PO=O,AO?APO,PO?APO,
∴BD⊥平面APO,
∵AP?APO,∴BD⊥PA….(6分)
(2)以O为原点,OA为x轴,OF为y轴,OP为z轴,建立坐标系
则$O(0,0,0),A(3\sqrt{3},0,0),P(0,0,\sqrt{3}),B(\sqrt{3},2,0)$,…(8分)
设$\vec n=(x,y,z)为平面OAP的一个法向量$,
则$\vec n=(0,1,0)$,$\vec m=(x,y,z)为平面ABP的一个法向量$,
$\overrightarrow{AB}$=(-2$\sqrt{3}$,2,0),$\overrightarrow{AP}$=(-3$\sqrt{3}$,0,$\sqrt{3}$),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AP}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2\sqrt{3}x+2y=0}\\{-3\sqrt{3}x+\sqrt{3}z=0}\end{array}\right.$,
令x=1,则y=$\sqrt{3}$,z=3,
则$\vec m=(1,\sqrt{3},3)$….(10分)
$cosθ=\frac{\vec m•\vec n}{{|{\vec m}||{\vec n}|}}=\frac{{\sqrt{3}}}{{\sqrt{13}}}$,
∴$tanθ=\frac{{\sqrt{30}}}{3}$…..(12分)
点评 本题主要考查线直线垂直的判定以及二面角的应用,建立坐标性,求出平面的法向量,利用向量法是解决本题的关键.综合性较强.

| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为“若x≠1,则 x2-3x+2≠0 | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 若 p∧q为假命题,则p,q均为假命题 | |
| D. | 对于命题 p:?x∈R使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0 |
| A. | [$\frac{1}{3}$,$\frac{1}{2}$) | B. | [$\frac{2}{5}$,$\frac{1}{2}$) | C. | [$\frac{2}{5}$,1) | D. | (0,$\frac{1}{2}$) |
| A. | α内有无数条直线都与β平行 | |
| B. | 直线a?α,直线b?β,且a∥β,b∥α | |
| C. | α内的任何直线都与β平行 | |
| D. | 直线a∥α,a∥β,且直线a不在α内,也不在β内 |
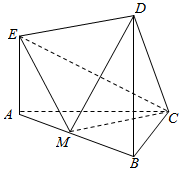 如图所示的几何体中,EA⊥平面ABC,BD⊥平面ABC,AC=BC=BD=2AE=$\frac{{\sqrt{2}}}{2}AB$,M是AB的中点.
如图所示的几何体中,EA⊥平面ABC,BD⊥平面ABC,AC=BC=BD=2AE=$\frac{{\sqrt{2}}}{2}AB$,M是AB的中点.