题目内容
已知棱长为1的正方体ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点.则以下结论不成立的是( )
| A、存在P,Q两点,使BP⊥DQ |
| B、存在P,Q两点,使BP,DQ与直线B1C都成45°的角 |
| C、若|PQ|=1,则四面体BDPQ的体积一定是定值 |
| D、若|PQ|=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:令P与A1点重合,Q与C1点重合,可判断A;根据BP与直线B1C所成的角最小值为45°,可判断B;根据平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥(其中O为上底面中心),可判断C;根据四面体BDPQ在该正方体六个面上的正投影的面积不变,可判断D.
解答:
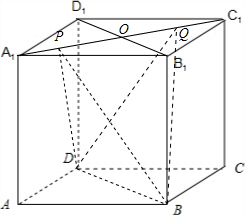 解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故A正确;
解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故A正确;
当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为45°,故B错误;
设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD,
平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥,故四面体BDPQ的体积一定是定值,故C正确;
四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度均为1的四边形,其面积为定值,
四面体BDPQ在四个侧面上的投影,均以上底为
,下底和高均为1的梯形,其面积为定值,
故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值,故D正确.
故选B.
 解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故A正确;
解:当P与A1点重合,Q与C1点重合时,BP⊥DQ,故A正确;当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为45°,故B错误;
设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD,
平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥,故四面体BDPQ的体积一定是定值,故C正确;
四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度均为1的四边形,其面积为定值,
四面体BDPQ在四个侧面上的投影,均以上底为
| ||
| 2 |
故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值,故D正确.
故选B.
点评:本题考查的知识点是棱柱的几何特征,和空间异面直线关系,棱锥体积,投影的综合应用.

练习册系列答案
相关题目
某养殖户有1万只鸭,因误食含有病毒的饲料而被感染,已知该病的发病率为0.001,设发病的鸭的只数为ξ,则D(ξ)等于( )
| A、1 | B、9.99 |
| C、10 | D、19.6 |
函数f(x)=
x5+
x3在R上有( )个极值点.
| 1 |
| 5 |
| 1 |
| 3 |
| A、1个 | B、0个 | C、2个 | D、3个 |
某社区有400个家庭,其中高等收入家庭120户,中等收入家庭180户,低收入家庭100户.为了调查社会购买力的某项指标,要从中抽取一个容量为100的样本,记作①;某校高一年级有13名排球运动员,要从中选出3人调查学习负担情况,记作②.那么,完成上述2项调查宜采用的抽样方法是( )
| A、①用简单随机抽样,②用系统抽样 |
| B、①用分层抽样,②用简单随机抽样 |
| C、①用系统抽样,②用分层抽样 |
| D、①用分层抽样,②用系统抽样 |
下列函数中,x=0是极值点的函数是( )
| A、y=-x3 | ||
| B、y=-cosx | ||
| C、y=tanx-x | ||
D、y=
|
已知(1+2x)n的展开式中所有系数之和等于729,那么这个展开式中x3项的系数是( )
| A、56 | B、160 |
| C、80 | D、180 |
函数y=(x-1)2的导数是( )
| A、-2 |
| B、(x-1)2 |
| C、2(x-1) |
| D、2(1-x) |