题目内容
8.已知函数f(x)=kx(k≠0),对于任意的x都满足f(x-1)•f(x)=x2-x,函数g(x)=ax(a>0,且a≠1)(1)求函数f(x)的解析式;
(2)已知关于x的方程g(2x+1)=f(x+1).f(x)恰有一实数解为x0,且,x0∈($\frac{1}{4}$,$\frac{1}{2}$).求实数a的取值范围.
分析 (1)根据f(x-1)•f(x)=x2-x列出恒等式,得出k;
(2)根据g(2x+1)=f(x+1)•f(x)得a2x+1=x2+x.作出函数图象,根据x0的范围列出不等式解出.
解答 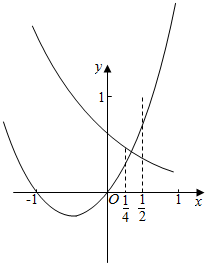 解:(1)∵f(x-1)•f(x)=x2-x,
解:(1)∵f(x-1)•f(x)=x2-x,
∴k(x-1)•kx=x2-x,
即k2x2-k2x=x2-x,∴k2=1,k=1或k=-1.
∴f(x)=x或f(x)=-x.
(2)f(x+1)•f(x)=(x+1)2-(x+1)=x2+x,g(2x+1)=a2x+1,∴a2x+1=x2+x.
作出y=a2x+1与y=x2+x的函数图象,如图所示:
∵a2x+1=x2+x.有唯一解x0,且x0∈($\frac{1}{4}$,$\frac{1}{2}$).∴0<a<1.
∴$\left\{\begin{array}{l}{{a}^{\frac{3}{2}}>(\frac{1}{4})^{2}+\frac{1}{4}}\\{{a}^{2}<{(\frac{1}{2})}^{2}+\frac{1}{2}}\end{array}\right.$,解得$(\frac{5}{16})^{\frac{2}{3}}$<a<$\frac{\sqrt{3}}{2}$.
∴实数a的取值范围是($(\frac{5}{16})^{\frac{2}{3}}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了函数解析式的求解,函数的零点与函数图象的关系,走出符合条件的函数图象是解题关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
18.在复平面内,复数z=(|a|-1)+(a+1)i(a∈R,i为虚数单位)对应的点位于第四象限的充要条件是( )
| A. | a≥-1 | B. | a>-1 | C. | a≤-1 | D. | a<-1 |
19.某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
| A. | 800 | B. | 900 | C. | 1000 | D. | 1100 |
16.已知sin($\frac{π}{4}$-x)=$\frac{4}{5}$,则sin2x=( )
| A. | $\frac{18}{25}$ | B. | $\frac{7}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{16}{25}$ |
3.从集合A={2,3,-4}中随机选取一个数记为k,则函数y=kx为单调递增的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
20.已知函数f(x)的图象是连续不断的,有如下的对应值表:
则函数y=f(x)在区间[1,6]上的零点至少有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 123.56 | 21.45 | -7.82 | 11.45 | -53.76 | -128.88 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
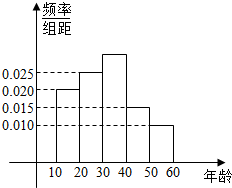 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.