题目内容
若实数a,b,c成等比数列,非零实数x,y分别为a与b,b与c的等差中项,则下列结论正确的是( )
A、
| ||||
B、
| ||||
| C、ax+cy=1 | ||||
| D、ax+cy=2 |
考点:等差数列的性质,等比数列的性质
专题:计算题,等差数列与等比数列
分析:由等比数列与等差数列的性质可得:b2=ac,2x=a+b,2y=b+c,代入
+
,化简即可得出.
| a |
| x |
| c |
| y |
解答:
解:∵实数a,b,c成等比数列,非零x,y实数分别是a,b和b,c的等差中项,
∴b2=ac,2x=a+b,2y=b+c,
∴
+
=
+
=
=2.
故选:B.
∴b2=ac,2x=a+b,2y=b+c,
∴
| a |
| x |
| c |
| y |
| 2a |
| a+b |
| 2c |
| b+c |
| 2(ab+ac+ac+bc) |
| ab+ac+ac+bc |
故选:B.
点评:本题考查了等比数列与等差数列的性质,属于基础题.

练习册系列答案
相关题目
已知F1、F2是离心率为
的双曲线C的左、右焦点,点P在C上,若|PF1|=2|PF2|,则cos∠F1PF2=( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线C:
-
=1(b>0)的一条渐进线方程为y=
x,F1,F2分别为双曲线C的左右焦点,P为双曲线C上的一点,满足|PF1|:|PF2|=3:1,则|
+
|的值是( )
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| A、4 | ||||
B、2
| ||||
C、2
| ||||
D、
|
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第2014次互换座位后,小兔坐在第( )号座位上.
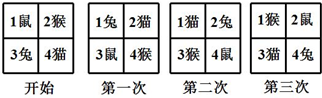

| A、1 | B、2 | C、3 | D、4 |
某款手机的广告宣传费用x(单位万元)与利润y(单位万元)的统计数据如下表:
根据上表可得线性回归方程
=
x+
中的
为9.4,据此模型预报广告宣传费用为10万元时利润为( )
| 广告宣传费用x | 6 | 5 | 7 | 8 |
| 利润y | 34 | 26 | 38 | 42 |
 |
| y |
 |
| b |
 |
| a |
| ? |
| b |
| A、65.0万元 |
| B、67.9万元 |
| C、68.1万元 |
| D、68.9万元 |
若函数f(x)=xlnx-a有两个零点,则实数a的取值范围为( )
A、[0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
曲线
+
=1与
+
=1(k<9)有相同的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴 | B、准线 | C、焦点 | D、离心率 |