题目内容

已知向量
a
，
b
满足|
b
|=2|
a
|，
b
-
a
与2
a
+
b
的夹角为
π
3
，则
a
，
b
的夹角是（　　）
A、
π
6
B、
π
3
C、
2π
3
D、
5π
6
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：由
b
-
a
与2
a
+
b
的夹角为
π
3
求得
a
2=
a
•
b
，设
a
，
b
的夹角为θ，则根据cosθ=
a
•
b
|
a
|•|
b
|
的值，求得θ的值．
解答： 解：∵
b
-
a
与2
a
+
b
的夹角为
π
3
，且|
b
|=2|
a
|，
则有cos
π
3
=
1
2
=
(
b
-
a
)•(2
a
+
b
)
(
b
-
a
)2
(2
a
+
b
)2
=
2
a
2+
a
•
b
(5
a
2-2
a
•
b
)(8
a
2+4
a
•
b
)
，
得
a
2=
a
•
b
，设
a
，
b
的夹角为θ，则cosθ=
a
•
b
|
a
||
b
|
=
1
2
，则θ=
π
3
，
故选：B．
点评：本题主要考查用两个向量的数量积表示两个向量的夹角，根据三角函数的值求角，属于基础题．
练习册系列答案
相关题目
如图所示，一个三棱锥的三视图中，其俯视图是正三角形，主视图及左视图的轮廓都是直角三角形，若这个三棱锥的四个顶点都在一个球的球面上，则这个球的体积为
 
．
若集合A={x|
1
x
＜1}，B={x||x|＜2}，则A∩B=
 
．
过原点作圆x2+（y-6）2=9的两条切线，则该圆夹在两条切线间的劣弧长为（　　）
A、πB、2πC、4πD、6π
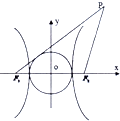如图，点P在双曲线
x2
a2
-
y2
b2
=1的右支上，F1，F2分别是双曲线的左右焦点，|PF2|=|F1F2|，直线PF1与圆x2+y2=a2相切，则双曲线的离心率e（　　）
A、
4
3
B、
5
3
C、
3
D、2
向量
a
=（cosα，sinα），
b
=（cosx，sinx），若函数f（x）=
a
•
b
是奇函数，则α可以是（　　）
A、0
B、
π
4
C、
π
3
D、
π
2
已知命题p：函数f（x）=|sin2x-
1
2
|的最小正周期为π；命题q：若函数f（x+1）为偶函数，则f（x）关于x=1对称．则下列命题是真命题的是（　　）
A、p∧q
B、p∨q
C、（￢p）∧（￢q）
D、p∨（￢q）
已知i为虚数单位，则i（1-i）等于（　　）
A、1-iB、-1+i
C、-1-iD、1+i
已知集合A={1，zi}，B={2}，i为虚数单位，若A∩B=B，则纯虚数z为（　　）
A、-iB、-2iC、iD、2i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网