题目内容
如图，如图，A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，则CD=考点：与圆有关的比例线段
专题：直线与圆
分析：由题设条件推导出OC=CA=1，OB=2，BC=
，由相交弦定理得（2+1）•（2-1）=BC•CD，由此能求出CD．
| 5 |
解答：
解：如图，∵A，B是圆O上的两点，且OA⊥OB，OA=2，
C为OA的中点，连接BC并延长交圆O于点D，
∴OC=CA=1，OB=2，
∴BC=
=
，
∴由相交弦定理得（2+1）•（2-1）=BC•CD，
∴CD=
=
．
故答案为：
．
如图，∵A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，
∴OC=CA=1，OB=2，
∴BC=
| 22+12 |
| 5 |
∴由相交弦定理得（2+1）•（2-1）=BC•CD，
∴CD=
| 3 | ||
|
3
| ||
| 5 |
故答案为：
3
| ||
| 5 |
点评：本题考查与圆相关的线段长的求法，是中档题，解题时要认真审题，注意勾股定理和相交弦定理的合理运用．
练习册系列答案
相关题目
已知集合M={X∈N+|x2-x-6＜0}，i为虚数单位，复数z=
的实部，虚部，模分别为a，b，t，则下列选项正确的是（ ）
| 2 |
| 1+i |
| A、a+b∈M | B、t∈M |
| C、b∈M | D、a∈M |
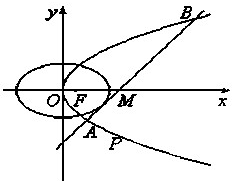如图所示，已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A，B两点．
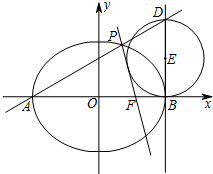已知椭圆C的中心在坐标原点，右焦点为F（1，0），A、B是椭圆C的左、右顶点，P是椭圆C上异于A、B的动点，且△APB面积的最大值为2