题目内容
已知函数f（x）=-x2+（m-2）x+2-m，且y=|f（x）|在[-1，0]上为单调减函数，则实数m的取值范围为 ．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：通过讨论判别式△的范围，得到不等式组，解出即可．
解答：
解：判别式△=m2-8m+12=（m-2）（m-6），
①当△≤0时，即2≤m≤6时，函数f（x）≤0恒成立，
∴|f（x）|=-f（x）=x2-（m-2）x+m-2，
对称轴方程为：x=
，
∴当
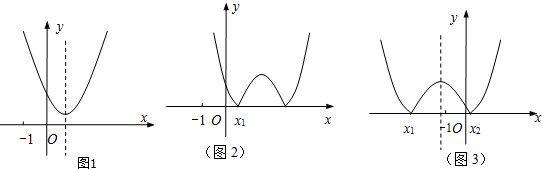
≥0即m≥2时符合题意（如图1），
此时2≤m≤6；
②当△＞0时，即m＜2或m＞6时，
方程f（x）=0的两个实根为x=
，
不妨设x1＜x2，由题意及图象得x1≥0 或
，
即m-2≥
（如图2）或
（如图3）
解得m≥2或m≤0，此时m≤0或m＞6，
综上得m的取值范围是：m≤0或m≥2；
故答案为：m≤0或m≥2．
①当△≤0时，即2≤m≤6时，函数f（x）≤0恒成立，
∴|f（x）|=-f（x）=x2-（m-2）x+m-2，
对称轴方程为：x=
| m-2 |
| 2 |
∴当
| m-2 |
| 2 |
此时2≤m≤6；
②当△＞0时，即m＜2或m＞6时，
方程f（x）=0的两个实根为x=
(m-2)±
| ||
| 2 |
不妨设x1＜x2，由题意及图象得x1≥0 或
|
即m-2≥
| m2-8m+12 |
|
解得m≥2或m≤0，此时m≤0或m＞6，
综上得m的取值范围是：m≤0或m≥2；
故答案为：m≤0或m≥2．
点评：本题考查了函数的单调性问题，考查了数形结合思想，分类讨论思想，是一道中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
（1）画出函数f（x）=|x|（x-4）的图象；定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f（x）=x2-2x，若x∈[-4，-2]时，f（x）≥
(
-t)恒成立，则实数t的取值范围是（ ）
| 1 |
| 8 |
| 3 |
| t |
| A、（-∞，-1]∪（0，3] | ||||
B、(-∞，-
| ||||
| C、[-1，0）∪[3，+∞） | ||||
D、[-
|
函数y=cos（2x-
）的图象的一条对称轴方程是（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
| D、x=π |