题目内容
16．已知公差为2的等差数列{an}及公比为2的等比数列{bn}满足a1+b1＞0，a2+b2＜0，则a3+b3的取值范围是（-∞，-2）．分析 由题意列关于a1、b1的不等式组，再把a3+b3转化为含有a1、b1的线性目标函数，利用线性规划知识求得a3+b3的取值范围．
解答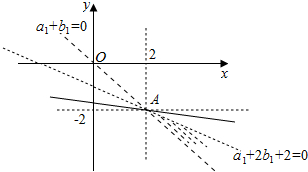 
解：由题意可得，a1+2+2b1＜0，
又a1+b1＞0，∴2+b1=-（a1+b1）＜0，
则b1＜-2，∴-b1＞2，
则a1＞-b1＞2．
∴约束条件为$\left\{\begin{array}{l}{{a}_{1}＞2}\\{{b}_{1}＜-2}\\{{a}_{1}+{b}_{1}＞0}\\{{a}_{1}+2{b}_{1}+2＜0}\end{array}\right.$，
目标函数z=a3+b3=a1+4b1+4．
由约束条件作出可行域如图：
化目标函数为${b}_{1}=-\frac{{a}_{1}}{4}+\frac{z}{4}-1$，
由图可知，当直线${b}_{1}=-\frac{{a}_{1}}{4}+\frac{z}{4}-1$过A（2，-2）时，直线在y轴上的截距最大，
z有最大值为2+4×（-2）+4=-2．
故答案为：（-∞，-2）．
点评 本题是等差数列与等比数列的综合题，考查数学转化思想方法和数形结合的数学思想方法，是中档题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目