题目内容
设Sn是数列{an}的前n项和,已知an=2n2+2n,则Sn= .
考点:数列的求和
专题:等差数列与等比数列
分析:利用分组求和法求解.
解答:
解:∵an=2n2+2n,
∴Sn=2(12+22+32+…+n2)+2(1+2+3+…+n)
=2×
+2×
=
+n(n+1).
故答案为:
+n(n+1).
∴Sn=2(12+22+32+…+n2)+2(1+2+3+…+n)
=2×
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
=
| n(n+1)(2n+1) |
| 3 |
故答案为:
| n(n+1)(2n+1) |
| 3 |
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
在平行四边形ABCD中,
+
等于( )
| AB |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、|
|
 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.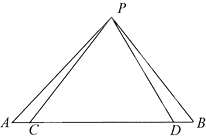 如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为
如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为