题目内容
17.已知cos($\frac{π}{4}$+α)=$\frac{1}{3}$,α∈(0,$\frac{π}{2}$),则cos($\frac{π}{12}$-α)=$\frac{1+2\sqrt{6}}{6}$.分析 由角的范围,根据同角三角函数基本关系式可求sin($\frac{π}{4}$+α)的值,由角的关系,利用诱导公式,特殊角的三角函数值,两角和的正弦函数公式化简所求即可求值.
解答 解:∵cos($\frac{π}{4}$+α)=$\frac{1}{3}$,α∈(0,$\frac{π}{2}$),
∴$\frac{π}{4}$+α∈($\frac{π}{4}$,$\frac{3π}{4}$),
∴sin($\frac{π}{4}$+α)=$\sqrt{1-cos(\frac{π}{4}+α)^{2}}$=$\frac{2\sqrt{2}}{3}$,
∴cos($\frac{π}{12}$-α)
=sin[$\frac{π}{2}$-($\frac{π}{12}$-α)]
=sin($\frac{5π}{12}$+α)
=sin[$\frac{π}{6}$+($\frac{π}{4}$+α)]
=sin$\frac{π}{6}$cos($\frac{π}{4}$+α)+cos$\frac{π}{6}$sin($\frac{π}{4}$+α)
=$\frac{1}{2}×\frac{1}{3}$+$\frac{\sqrt{3}}{2}×\frac{2\sqrt{2}}{3}$
=$\frac{1+2\sqrt{6}}{6}$.
故答案为:$\frac{1+2\sqrt{6}}{6}$.
点评 本题主要考查了同角三角函数基本关系式,诱导公式,特殊角的三角函数值,两角和的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
5.如图程序中,若输入x=-2,则输出y的值为( )
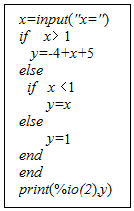
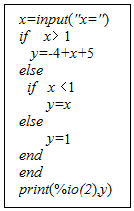
| A. | 1 | B. | 13 | C. | -2 | D. | -3 |
6.若$\overrightarrow{O{F}_{1}}$=(2,2),$\overrightarrow{O{F}_{2}}$=(-2,3)分别表示F1,F2,则|F1+F2|=( )
| A. | (0,5) | B. | 25 | C. | 2$\sqrt{2}$ | D. | 5 |