题目内容
曲线y=x2,x=0,y=1,所围成的图形的面积可用定积分表示为 .
考点:定积分在求面积中的应用
专题:导数的概念及应用
分析:根据积分的几何意义即可得到结论.
解答:
解: 作出对应的图形如图:
作出对应的图形如图:
则两个图象的交点横坐标分别为0和1,
∴根据积分的几何意义可知,所围成的图形的面积可用定积分表示为:
(1-x2)dx.
故答案为:
(1-x2)dx.
 作出对应的图形如图:
作出对应的图形如图:则两个图象的交点横坐标分别为0和1,
∴根据积分的几何意义可知,所围成的图形的面积可用定积分表示为:
| ∫ | 1 0 |
故答案为:
| ∫ | 1 0 |
点评:本题主要考查积分的应用,根据图象确定积分的上限和下限是解决本题的关键.

练习册系列答案
相关题目
下列可能是三进制数的是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
设f(x)=ex+x-4,则函数f(x)=0的解位于区间( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
直线2x-3y+1=0和x-3=0的夹角是( )
A、π-arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
极坐标方程ρcosθ=4表示的曲线是( )
| A、一条平行于极轴的直线 |
| B、一条垂直于极轴的直线 |
| C、圆心在极轴上的圆 |
| D、过极点的圆 |
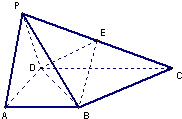 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.