题目内容
函数y=
的值域为 ．
| -x2-4x+5 |
考点：函数的值域
专题：函数的性质及应用
分析：将-x2-4x+5配方后即可得到
的最大值和最小值，从而求出该函数的值域．
| -x2-4x+5 |
解答：
解：y=
=
；
∴0≤
≤
=3，即0≤y≤3；
∴函数y=
的值域为[0，3]．
故答案为：[0，3]．
| -x2-4x+5 |
| -(x+2)2+9 |
∴0≤
| -(x+2)2+9 |
| 9 |
∴函数y=
| -x2-4x+5 |
故答案为：[0，3]．
点评：考查通过配方求二次函数最值的方法，以及被开方数大于等于0．
练习册系列答案
相关题目
函数y=（m+1）x-（4m-3）的图象在第一、二、四象限，那么m的取值范围是（ ）
A、m＜
| ||
B、-1＜m＜
| ||
| C、m＜-1 | ||
| D、m＞-1 |
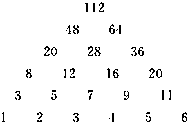给定正整数n（n≥2）按下图方式构成三角形数表；第一行依次写上数1，2，3，…，n，在下面一行的每相邻两个数的正中间上方写上这两个数之和，得到上面一行的数（比下一行少一个数），依此类推，最后一行（第n行）只有一个数．例如n=6时数表如图所示，则当n=2007时最后一行的数是 （ ）| A、251×22007 |
| B、2007×22006 |
| C、251×22008 |
| D、2007×22005 |
设f（x）=
且f（2）=1，则f（1）=（ ）
|
| A、2 | B、4 | C、6 | D、8 |