题目内容
解不等式:x2+
x+
≤0.
| 2 |
| 3 |
| 1 |
| 9 |
考点:一元二次不等式的解法
专题:计算题,不等式的解法及应用
分析:将不等式的左边配方,由平方数非负,转化为解方程即可得到解集.
解答:
解:x2+
x+
≤0即为
(x+
)2≤0,
但(x+
)2≥0,
则有(x+
)2=0,
解得x=-
,
则解集为{-
}.
| 2 |
| 3 |
| 1 |
| 9 |
(x+
| 1 |
| 3 |
但(x+
| 1 |
| 3 |
则有(x+
| 1 |
| 3 |
解得x=-
| 1 |
| 3 |
则解集为{-
| 1 |
| 3 |
点评:本题考查二次不等式的解法,考查配方法的运用,考查运算能力,属于基础题.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
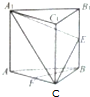 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.