题目内容
数列{an}满足an+1=3an,(n∈N*),且a1=3
(1)求数列{an}的通项公式an;
(2)数列{bn}满足bn=log3an,(n∈N*),记cn=an+bn,(n∈N*),求数列{cn}的前n项和Sn.
(1)求数列{an}的通项公式an;
(2)数列{bn}满足bn=log3an,(n∈N*),记cn=an+bn,(n∈N*),求数列{cn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)根据an+1=3an,(n∈N*),可得
=3,数列{an}是首项为3,公比为3的等比数列,据此求出通项公式an即可;
(2)首先根据cn=an+bn,(n∈N*),求出数列{cn}的通项公式,然后求出数列{cn}的前n项和Sn即可.
| an+1 |
| an |
(2)首先根据cn=an+bn,(n∈N*),求出数列{cn}的通项公式,然后求出数列{cn}的前n项和Sn即可.
解答:
解:(1)根据an+1=3an,(n∈N*),
可得
=3,
所以数列{an}是首项为3,公比为3的等比数列,
则an=3×3n-1=3n(n∈N*);
(2)∵bn=log3an=log33n=n,cn=an+bn,
∴cn=3n+n
∴数列{cn}的前n项和为:
Sn=(31+32+…+3n)+(1+2+3+…+n)
=
+
=
.
可得
| an+1 |
| an |
所以数列{an}是首项为3,公比为3的等比数列,
则an=3×3n-1=3n(n∈N*);
(2)∵bn=log3an=log33n=n,cn=an+bn,
∴cn=3n+n
∴数列{cn}的前n项和为:
Sn=(31+32+…+3n)+(1+2+3+…+n)
=
| 3(1-3n) |
| 1-3 |
| n(n+1) |
| 2 |
=
| 3n+1+n2+n-3 |
| 2 |
点评:本题主要考查了等比数列的通项公式的应用,考查了数列的求和,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC利用斜二测画法得到的水平放置的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴,若△A′B′C′的面积是3,则原△ABC的面积为( )
如图,△ABC利用斜二测画法得到的水平放置的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴,若△A′B′C′的面积是3,则原△ABC的面积为( )
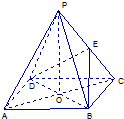 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长AB=1,E是PC的中点.