题目内容
9.设函数f(x)=lg(x2-x)-lg(x-1).且f(x0)=2.则x0=100.分析 f(x0)=2,⇒lg(x02-x0)-lg(x0-1)=2.$\frac{{x}_{0}({x}_{0}-1)}{{x}_{0}-1}={e}^{2}$,且${{x}_{0}}^{2}-{x}_{0}>0,{x}_{0}-1>0$,解得x0,
解答 解:f(x0)=2,⇒lg(x02-x0)-lg(x0-1)=2,
∴$\frac{{x}_{0}({x}_{0}-1)}{{x}_{0}}=1{0}^{2}$
且${{x}_{0}}^{2}-{x}_{0}>0,{x}_{0}-1>0$,解得x0=100,
经检验符合题意.故答案为:100.
点评 本题考查了对数型方程的解法,对数的运算性质,属于基础题.

练习册系列答案
相关题目
17.已知向量$\overrightarrow a•(\overrightarrow a+2\overrightarrow b)=0$,$|\overrightarrow a|=|\overrightarrow b|=2$,则向量$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
4.一个袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和小于15的概率为( )
| A. | $\frac{29}{32}$ | B. | $\frac{63}{64}$ | C. | $\frac{31}{32}$ | D. | $\frac{61}{64}$ |
18.已知角α的终边过点$P(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,则sinα=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
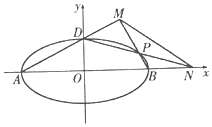 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.