题目内容
12.已知二次函数f(x)=ax2+bx+c(a,b,c为常数,且a≠0),满足条件f(0)=0,f(1+x)=f(1-x)恒成立,且方程f(x)=x有两个相等的实数根.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别是[m,n]和[3m,3n],如果存在,求出m,n的值;如果不存在,请说明理由.
分析 (Ⅰ)由题意:f(0)=0,f(1+x)=f(1-x)恒成立,且方程f(x)=x有两个相等的实数根.△=0,可求a,b,c的值,可得解析式
(Ⅱ)(m<n),f(x)的定义域和值域分别是[m,n]和[3m,3n],利用单调性求解.
解答 解:(Ⅰ)因为二次函数f(x)=ax2+bx+c,满足条件f(0)=0,∴c=0,
又 f(1+x)=f(1-x)恒成立,∴函数f(x)的图象关于直线x=1对称,
而二次函数的对称轴为$x=-\frac{b}{2a}$,∴$-\frac{b}{2a}=1$①
又方程f(x)=x有等根,即 ax2+(b-1)x=0有等根.∴△=(b-1)2=0②
由①②得 $b=1,\;\;a=-\frac{1}{2}$,
∴函数f(x)的解析式$f(x)=-\frac{1}{2}{x^2}+x$.
(Ⅱ)由(Ⅰ)可得$f(x)=-\frac{1}{2}{x^2}+x=-\frac{1}{2}{(x-1)^2}+\frac{1}{2}≤\frac{1}{2}$,
对称轴x=1,
如果存在满足条件的m,n,则必需$3n≤\frac{1}{2}$,∴$n≤\frac{1}{6}$,
从而$m<n≤\frac{1}{6}<1$,而x≤1时,f(x)单调递增,
∴$\left\{{\begin{array}{l}{f(m)=-\frac{1}{2}{m^2}+m=3m}\\{f(n)=-\frac{1}{2}{n^2}+n=3n}\end{array}}\right.$,解得 m=-4,n=0.
所以,存在m=-4,n=0满足条件.
点评 本题考查二次函数的解析式的求法和性质的运用.属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
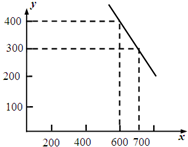 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).