题目内容
9.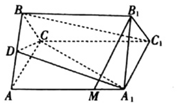 如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.
如图,在正三棱柱ABC-A1B1C1中,点D是AB中点,M是AA1上一点,且AM=tAA1.(1)求证:BC1∥平面A1CD;
(2)若3AB=2AA1,当t为何值时,B1M⊥平面A1CD?
分析 (1)取A1B1的中点E,连接BE,C1E.只需证明,面EBC1∥平面A1CD;即可得到BC1∥平面A1CD.
(2)易得CD⊥B1M,要使B1M⊥平面A1CD,只需DA1⊥MB即可,如下图,当DA1⊥MB时,△ADA1∽△A1MB1,⇒$\frac{AD}{{A}_{1}M}=\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$,即可求得t.
解答 解:(1)如图1,取A1B1的中点E,连接BE,C1E.
在正三棱柱ABC-A1B1C1中,点D是AB中点,可得CD∥C1E
又因为DB∥EA1,DB=EA1⇒BE∥DA1.
且CD∩DA1=D,BE∩C1E=E,面EBC1∥平面A1CD;
∵BC1?面EBC1,BC1?平面A1CD,∴BC1∥平面A1CD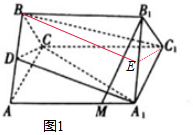
(2)由在正三棱柱ABC-A1B1C1中,点D是AB中点,可得CD⊥面AA1B1B.
⇒CD⊥B1M,
∴要使B1M⊥平面A1CD,只需DA1⊥MB即可,如下图,
当DA1⊥MB时,△ADA1∽△A1MB1,
⇒$\frac{AD}{{A}_{1}M}=\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$,又∵3AB=2AA1,DAB为中点
∴$\frac{\frac{1}{2}AB}{{A}_{1}M}=\frac{A{A}_{1}}{AB}=\frac{3}{2}$⇒${A}_{1}M=\frac{1}{3}AB=\frac{1}{3}×\frac{2}{3}A{A}_{1}=\frac{2}{9}A{A}_{1}$
∴$AM=\frac{7}{9}A{A}_{1}$
即当t=$\frac{7}{9}$时,B1M⊥平面A1CD.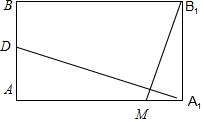
点评 本题考查了空间线面平行的判定,线面垂直的判定,属于中档题.

练习册系列答案
相关题目
14.下列函数中既是偶函数,又在区间(0,1)上单调递增的是( )
| A. | y=cosx | B. | $y={x^{\frac{1}{2}}}$ | C. | y=2|x| | D. | y=|lgx| |
1.在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
(Ⅰ)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程y=$\widehatbx+a$;
(Ⅱ)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y-0.05x2-1.4,请结合(Ⅰ)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
参考公式:$\widehat{y}$=$\widehat{b}$x+a,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{\;}({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x(个) | 2 | 3 | 4 | 5 | 6 |
| y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅱ)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y-0.05x2-1.4,请结合(Ⅰ)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
参考公式:$\widehat{y}$=$\widehat{b}$x+a,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{\;}({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
18. 某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
 某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )| A. | 44,45,56 | B. | 44,43,56 | C. | 44,43,57 | D. | 45,43,57 |
19.已知i是虚数单位,则满足z-i=|1+2i|的复数z在复平面上对应点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |