题目内容
已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2-x,设函数f(x)的值域为集合A.
(Ⅰ)求函数f(x)的解析式和集合A;
(Ⅱ)设函数g(x)=lg[-x2+(a-1)x+a]的定义域为集合B,且A⊆B,求实数a的取值范围.
(Ⅰ)求函数f(x)的解析式和集合A;
(Ⅱ)设函数g(x)=lg[-x2+(a-1)x+a]的定义域为集合B,且A⊆B,求实数a的取值范围.
考点:函数奇偶性的性质,交集及其运算
专题:函数的性质及应用
分析:(Ⅰ)由已知的函数解析式结合函数为偶函数求得函数在x<0时的解析式,则函数在整个定义域中的解析式可求;
(Ⅱ)把函数g(x)=lg[-x2+(a-1)x+a]的定义域包含集合A转化为对于任意的x∈[0,1],-x2+(a-1)x+a>0恒成立,由此列不等式组求得a的取值范围.
(Ⅱ)把函数g(x)=lg[-x2+(a-1)x+a]的定义域包含集合A转化为对于任意的x∈[0,1],-x2+(a-1)x+a>0恒成立,由此列不等式组求得a的取值范围.
解答:
解:(Ⅰ)设x<0,则-x>0,由f(x)是偶函数,
∴f(x)=f(-x)=2x.
∴f(x)=
.
由f(x)=2-x,x≥0,得f(x)∈(0,1].
由f(x)=2x,x<0,得f(x)∈(0,1).
∴函数f(x)的值域集合A=[0,1];
(Ⅱ)函数g(x)=lg[-x2+(a-1)x+a]的定义域为集合B,且A⊆B,
说明对于任意的x∈[0,1],-x2+(a-1)x+a>0恒成立.
即
,解得:a>1.
∴实数a的取值范围是(1,+∞).
∴f(x)=f(-x)=2x.
∴f(x)=
|
由f(x)=2-x,x≥0,得f(x)∈(0,1].
由f(x)=2x,x<0,得f(x)∈(0,1).
∴函数f(x)的值域集合A=[0,1];
(Ⅱ)函数g(x)=lg[-x2+(a-1)x+a]的定义域为集合B,且A⊆B,
说明对于任意的x∈[0,1],-x2+(a-1)x+a>0恒成立.
即
|
∴实数a的取值范围是(1,+∞).
点评:本题考查了函数奇偶性的性质,考查了函数解析式的求法,训练了转化思想方法在解题中的应用,是中档题.

练习册系列答案
相关题目
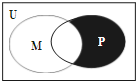 设全集U=Z,集合M={1,2}与P={x||x|<2,x∈Z}关系的韦恩(venn)图如图所示,则阴影部分所示的集合为( )
设全集U=Z,集合M={1,2}与P={x||x|<2,x∈Z}关系的韦恩(venn)图如图所示,则阴影部分所示的集合为( )| A、{-1,0} |
| B、{-2,-1,0} |
| C、{0,1,2} |
| D、{0,1} |
集合A={x|x2-2x>0},集合B是函数y=lg(2-x)的定义域,则A∩B=( )
| A、(-∞,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,+∞) |