题目内容
3.设集合S={1,2,3,…,n}(n≥5,n∈N*),集合A={a1,a2,a3}满足a1<a2<a3且a3-a2≤2,A⊆S(1)若n=6,求满足条件的集合A的个数;
(2)对任意的满足条件的n及A,求集合A的个数.
分析 (1)n=6时,可得出S={1,2,3,4,5,6},根据条件,可分别求出a3-a2=2,a3-a2=1时,集合A的个数,再求和即可;
(2)方法和过程同(1).
解答 解:(1)n=6时,S={1,2,3,4,5,6};
∵a3-a2≤2;
∴a3-a2=2,或a3-a2=1;
当a3-a2=2时,a2和a3可分别为2和4,3和5,4和6;
此时对应的a1分别有1个,2个和3个;
当a3-a2=1时,a2和a3可分别取2和3,3和4,4和5,5和6;
对应的a1分别有1个,2个,3个和4个;
∴集合A的个数=1+2+3+1+2+3+4=16个;
(2)当n≥5时,
若a3-a2=2,则a2和a3可分别为2和4,3和5,…,n-2和n;
此时,对应的a1可分别为1个,2个,…,n-3个,共有$\frac{(n-3)(n-2)}{2}$个;
同理,a3-a2=1时,a1共有$\frac{(n-2)(n-1)}{2}$个;
∴集合A的个数为:
$\frac{(n-3)(n-2)}{2}+\frac{(n-2)(n-1)}{2}$
=$\frac{2{n}^{2}-8n+8}{2}$
=(n-2)2,n≥5,n∈N*.
点评 考查列举法表示集合的概念和形式,分类讨论的方法,等差数列的求和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知点P(x,y)的坐标满足x2+y2-2y=0,则$u=\frac{y+1}{x}$的取值范围是( )
| A. | $-\sqrt{3}≤u≤\sqrt{3}$ | B. | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D. | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
8.一个无穷数列的前三项是1,2,3,下列不可以作为其通项公式的是( )
| A. | an=n | B. | an=n3-6n2+12n-6 | C. | an=$\frac{1}{2}$n2-$\frac{1}{2}$n+1 | D. | an=$\frac{6}{{n}^{2}-6n+11}$ |
15.抛物线y=4-x2与直线y=4x的两个交点为A、B,点P在抛物线上从A向B运动,当△PAB的面积为最大时,点P的坐标为( )
| A. | (-3,-5) | B. | (-2,0) | C. | (-1,3) | D. | (0,4) |
13.下列函数为奇函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x-1 | C. | y=x2 | D. | y=x3 |
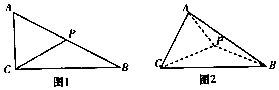 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.