Question

在圆的一条直径上，任取一点作与直径垂直的弦，则其弦长超过该圆的内接等边三角形的边长的概率为（　　）

• A、

  1

  4

• B、

  1

  3

• C、

  1

  2

• D、

  3

  2

Answer 1

考点：几何概型

专题：计算题,概率与统计

分析：由题意可得：要使弦长大于CD的长，就必须使圆心O到弦的距离小于|OF|，即可得出结论、

解答： 解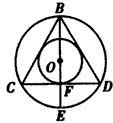：如图所示，△BCD是圆内接等边三角形，
过直径BE上任一点作垂直于直径的弦，
显然当弦为CD时就是△BCD的边长，
要使弦长大于CD的长，就必须使圆心O到弦的距离小于|OF|，
记事件A={弦长超过圆内接等边三角形的边长}，
由几何概型概率公式得P（A）=

1 2 ×2

2

=

1

2

，
即弦长超过圆内接等边三角形边长的概率是

1

2

．
故选：C．

点评：本题主要考查几何概型概率的计算，是简单题，确定得到各自的几何度量是解决问题的关键．