题目内容
8.已知F1、F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,由F1、F2分别作直线l:y=$\frac{2b}{\sqrt{3}a}$(x-1)的垂线段,垂足为M、N,若|MN|=$\sqrt{3}$c,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
分析 根据△CMF2∽△CF1N,建立比例关系,求出CM和MF2的大小,根据直角三角形建立方程关系进行求解即可.
解答 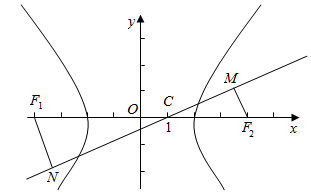 解:直线l:y=$\frac{2b}{\sqrt{3}a}$(x-1)过定点C(1,0),
解:直线l:y=$\frac{2b}{\sqrt{3}a}$(x-1)过定点C(1,0),
F1(-c,0),F2(c,0),不妨设c>1,
l:由y=$\frac{2b}{\sqrt{3}a}$(x-1)得2bx-$\sqrt{3}$a-2b=0,
则|FM2|=$\frac{|2bc-2b|}{\sqrt{4{b}^{2}+3{a}^{2}}}$,
则$\frac{CN}{CM}$=$\frac{C{F}_{1}}{C{F}_{2}}$=$\frac{c+1}{c-1}$,
则|CN|=$\frac{c+1}{c-1}$•|CM|,
∵|MN|=$\sqrt{3}$c,
∴|MN|=$\frac{c+1}{c-1}$•|CM|+|CM|=$\frac{2c}{c-1}$|CM|=$\sqrt{3}$c,
则|CM|=$\frac{\sqrt{3}}{2}$(c-1),
∵|CF2|2=|MF2|2+|CM|2,
∴(c-1)2=$\frac{4{b}^{2}(c-1)^{2}}{4{b}^{2}+3{a}^{2}}$+$\frac{3(c-1)^{2}}{4}$,
即$\frac{4{b}^{2}}{4{b}^{2}+3{a}^{2}}$=$\frac{1}{4}$,即16b2=4b2+3a2,
则a2=4b2=4(c2-a2),
即5a2=4c2,
即$\sqrt{5}$a=2c,
则e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,
故选:C.
点评 本题主要考查双曲线离心率的计算,根据三角形的相似性建立比例关系求出相应的线段长度,建立关于a,c的方程关系是解决本题的关键.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案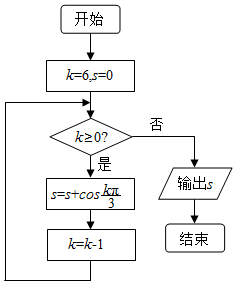 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
