题目内容
已知数列{an}的前n项和sn,点(n,sn)(n∈N*)在函数y=
x2+
x的图象上
(1)求{an}的通项公式
(2)设数列{
}的前n项和为Tn,不等式Tn>
loga(1-a)对任意的正整数恒成立,求实数a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求{an}的通项公式
(2)设数列{
| 1 |
| anan+2 |
| 1 |
| 3 |
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(1)Sn=
n2+
n,再写一式,即可求{an}的通项公式;
(2)由(1)知an=n,利用裂项法可求
=
(
-
),从而可求得Tn═
[(1-
)+(
-
)+(
-
)+…+(
-
)],由Tn+1-Tn=
>0,可判断数列{Tn}单调递增,从而可求得a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知an=n,利用裂项法可求
| 1 |
| anan+2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| (n+1)(n+3) |
解答:
解:(1)∵(n,Sn)在函数f(x)=
x2+
x的图象上,∴Sn=
n2+
n①
当n≥2时,Sn-1=
(n-1)2+
(n-1)②
①-②得an=n
当n=1时,a1=S1=
+
=1,符合上式,
∴an=n;
(2)由(1)知an=n,则
=
(
-
).
∴Tn═
[(1-
)+(
-
)+(
-
)+…+(
-
)]
=
(1+
-
-
)
=
-
(
+
).
∵Tn+1-Tn=
>0,
∴数列{Tn}单调递增,
∴(Tn)min=T1=
.
要使不等式Tn>
loga(1-a)对任意正整数n恒成立,只要
>
loga(1-a).
∵1-a>0,
∴0<a<1.
∴1-a>a,即0<a<
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
①-②得an=n
当n=1时,a1=S1=
| 1 |
| 2 |
| 1 |
| 2 |
∴an=n;
(2)由(1)知an=n,则
| 1 |
| anan+2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn═
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
∵Tn+1-Tn=
| 1 |
| (n+1)(n+3) |
∴数列{Tn}单调递增,
∴(Tn)min=T1=
| 1 |
| 3 |
要使不等式Tn>
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵1-a>0,
∴0<a<1.
∴1-a>a,即0<a<
| 1 |
| 2 |
点评:本题考查数列的通项与求和,着重考查等差关系的确定及数列{Tn}的单调性的分析,突出裂项法求和,突出转化思想与综合运算能力的考查,属于难题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
某扇形的圆心角为30°,半径为2,那么该扇形弧长为( )
A、
| ||
B、
| ||
C、
| ||
| D、60 |
已知
=(
,1),若将向量-2
绕坐标原点逆时针旋转120°得到向量
,则
的坐标为( )
| a |
| 3 |
| a |
| b |
| b |
| A、(0,4) | ||
B、(2
| ||
C、(-2
| ||
D、(2,-2
|
函数f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有( )
| A、e2013f(-2013)<f(0),f(2013)>e2013f(0) |
| B、e2013f(-2013)<f(0),f(2013)<e2013f(0) |
| C、e2013f(-2013)>f(0),f(2013)>e2013f(0) |
| D、e2013f(-2013)>f(0),f(2013)<e2013f(0) |
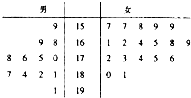 某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)
某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)