题目内容
10.公差不为0的等差数列{an}的部分项a${\;}_{{k}_{1}}$,a${\;}_{{k}_{2}}$,a${\;}_{{k}_{3}}$…构成等比数列{a${\;}_{{k}_{n}}$},且k1=1,k2=2,k3=6,则下列项中是数列{a${\;}_{{k}_{n}}$}中的项是( )| A. | a86 | B. | a84 | C. | a24 | D. | a20 |
分析 由已知得a1,a2,a6构成等比数列,由此得到等比数列的公比q=4,从而等比数列{a${\;}_{{k}_{n}}$}的通项公式为${a}_{{k}_{n}}$=${a}_{1}×{4}^{n-1}$,由此能求出结果.
解答 解:∵公差不为0的等差数列{an}的部分项a${\;}_{{k}_{1}}$,a${\;}_{{k}_{2}}$,a${\;}_{{k}_{3}}$…构成等比数列{a${\;}_{{k}_{n}}$},且k1=1,k2=2,k3=6,
∴a1,a2,a6构成等比数列,
∴(a1+d)2=a1(a1+5d),得d=3a1,
∴等比数列的公比q=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{{a}_{1}+3{a}_{1}}{{a}_{1}}$=4,
等差数列{an}的通项公式为an=a1+(n-1)×3a1=3a1n-2a1=(3n-2)a1,
等比数列{a${\;}_{{k}_{n}}$}的通项公式为${a}_{{k}_{n}}$=${a}_{1}×{4}^{n-1}$,
a86=a1+85d=256a1=${a}_{1}×{4}^{4}$,
a84=a1+83d=250a1,
a24=a1+23d=70a1,
a20=a1+19d=58a1,
∴a86是数列{a${\;}_{{k}_{n}}$}中的项.
故选:A.
点评 本题考查数列中某一项的判断,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
相关题目
1.设函数f(x)=x2+(2a-1)x+4,若x1<x2,x1+x2=2a时,有f(x1)>f(x2),则实数a的取值范围是( )
| A. | a$>\frac{1}{4}$ | B. | a$≥\frac{1}{4}$ | C. | a$<\frac{1}{4}$ | D. | a$≤\frac{1}{4}$ |
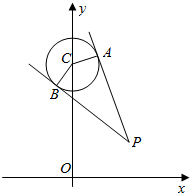 已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)