题目内容
20.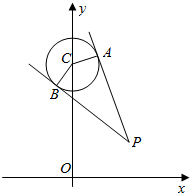 已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)(1)当P点坐标为(1,1)时,求PA;
(2)当P点坐标为(1,1)时,求f(P)的值;
(3)当P(x0,y0)在直线l:3x+4y-6=0上运动时,求f(P)最小值;
(4)当P(x0,y0)在圆(x+4)2+(y-1)2=4上运动时,指出f(P)的取值范围.
分析 (1)利用两点间的距离公式求PA;
(2)通过△PAC,△PBC是两个全等直角三角形求出f(P)的表达式,求出|PC|,即可求f(P)的值;
(3)当P(x0,y0)在直线3x+4y-6=0上运动时,利用点到直线的距离公式求出距离最小值,即可求f(P)最小值;
(4)当P(x0,y0)在圆(x+4)2+(y-1)2=4上运动时,求出|CD|,|PC|的范围,即可指出f(P)的取值范围.
解答 解:(1)当P点坐标为(1,1)时,C(0,4),∴PC=$\sqrt{10}$,∴PA=$\sqrt{P{C}^{2}-1}$=3;
(2)△PAC,△PBC是两个全等直角三角形,
∴f(P)=2S△PAC=|PA|•|AC|=|PA|=3;
(3)P(x0,y0)在直线3x+4y-6=0上运动时,|PC|的最小值为点C到直线3x+4y-6=0的距离d,d=2,
∴f(P)的最小值为$\sqrt{3}$;
(4)P(x0,y0)在圆D:(x+4)2+(y-1)2=4上运动时,|CD|=5,
|PC|∈[3,7],f(P)∈[2$\sqrt{2}$,4$\sqrt{3}$].
点评 本题考查直线与圆的位置关系,点到直线的距离函数表达式值的范围的求法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
10.公差不为0的等差数列{an}的部分项a${\;}_{{k}_{1}}$,a${\;}_{{k}_{2}}$,a${\;}_{{k}_{3}}$…构成等比数列{a${\;}_{{k}_{n}}$},且k1=1,k2=2,k3=6,则下列项中是数列{a${\;}_{{k}_{n}}$}中的项是( )
| A. | a86 | B. | a84 | C. | a24 | D. | a20 |
15.不等式5x2-3x-8>0的解集为( )
| A. | (-1,$\frac{8}{5}$) | B. | (-∞,-1)∪($\frac{8}{5}$,+∞) | C. | ∅ | D. | R |
9.若a>1,b<0,且ab+a-b=2$\sqrt{3}$,则ab-a-b的值等于( )
| A. | ±2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | 2 |